四川省绵阳市2019届高三文数第三次诊断性考试试卷
试卷更新日期:2019-08-19 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 已知 为虚数单位,复数 满足 ,则 ( )A、 B、 C、 D、3. 中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是 年和 年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
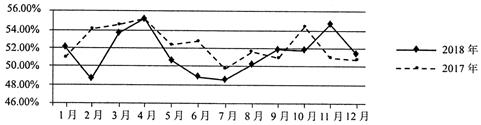 A、 年 月至 月的仓储指数比 年同期波动性更大 B、 年、 年的最大仓储指数都出现在 月份 C、 年全年仓储指数平均值明显低于 年 D、 年各月仓储指数的中位数与 年各月仓储指数中位数差异明显4. 函数 的图象在 处的切线斜率为( )A、 B、 C、 D、5. 将函数 的图象向左平移 个单位,得到函数 的图象,则 的解析式为( )A、 B、 C、 D、6. 下列函数中,既是奇函数,又在 上是增函数的是( )A、 B、 C、 D、7. 已知变量 , 满足 则 的最大值为( )A、 B、 C、 D、8. 已知一个封闭的长方体容器中装有两个大小相同的铁球,若该长方体容器的三个相邻侧面的面积分别为 , , ,则铁球的直径最大只能为( )A、 B、 C、 D、9. 已知双曲线 : 的两个焦点分别为 , ,以原点 为圆心, 为半径作圆,与双曲线 相交.若顺次连接这些交点和 , 恰好构成一个正六边形,则双曲线 的离心率为( )A、 B、 C、 D、10. 在 中, 分别为角 的对边,若 ,且 的面积 ,则 ( )A、 B、 C、 D、11. 已知抛物线 : 的焦点为 ,点 ,直线 与抛物线 交于点 ( 在第一象限内),与其准线交于点 ,若 ,则点 到 轴距离为( )A、 B、 C、 D、12. 若 ,且 , , ,则 的值是( )A、 B、 C、 D、
A、 年 月至 月的仓储指数比 年同期波动性更大 B、 年、 年的最大仓储指数都出现在 月份 C、 年全年仓储指数平均值明显低于 年 D、 年各月仓储指数的中位数与 年各月仓储指数中位数差异明显4. 函数 的图象在 处的切线斜率为( )A、 B、 C、 D、5. 将函数 的图象向左平移 个单位,得到函数 的图象,则 的解析式为( )A、 B、 C、 D、6. 下列函数中,既是奇函数,又在 上是增函数的是( )A、 B、 C、 D、7. 已知变量 , 满足 则 的最大值为( )A、 B、 C、 D、8. 已知一个封闭的长方体容器中装有两个大小相同的铁球,若该长方体容器的三个相邻侧面的面积分别为 , , ,则铁球的直径最大只能为( )A、 B、 C、 D、9. 已知双曲线 : 的两个焦点分别为 , ,以原点 为圆心, 为半径作圆,与双曲线 相交.若顺次连接这些交点和 , 恰好构成一个正六边形,则双曲线 的离心率为( )A、 B、 C、 D、10. 在 中, 分别为角 的对边,若 ,且 的面积 ,则 ( )A、 B、 C、 D、11. 已知抛物线 : 的焦点为 ,点 ,直线 与抛物线 交于点 ( 在第一象限内),与其准线交于点 ,若 ,则点 到 轴距离为( )A、 B、 C、 D、12. 若 ,且 , , ,则 的值是( )A、 B、 C、 D、二、填空题
-
13. 函数 则 .14. 已知 , 是第二象限的角,则 .15. 已知 的面积为 ,且 ,则 .16. 在《九章算术》中有称为“羡除”的五面体体积的求法.现有一个类似于“羡除”的有三条棱互相平行的五面体,其三视图如图所示,则该五面体的体积为 .

三、解答题
-
17. 已知数列 满足 , .(1)、求证:数列 是等差数列;(2)、若 ,求数列 的前 项和 .18. 目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
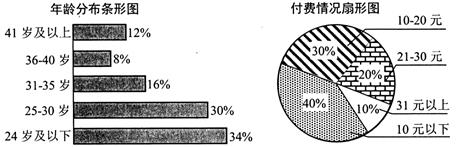
有声书公司将付费高于 元的用户定义为“爱付费用户”,将年龄在 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有 的“年轻用户”是“爱付费用户”.
(1)、完成下面的 列联表,并据此资料,能否有 的把握认为用户“爱付费”与其为“年轻用户”有关?爱付费用户
不爱付费用户
合计
年轻用户
非年轻用户
合计
(2)、若公司采用分层抽样方法从“爱付费用户”中随机选取 人,再从这 人中随机抽取 人进行访谈,求抽取的 人恰好都是“年轻用户”的概率..
19. 如图,在四棱锥 中,底面 是菱形,平面 平面 ,且 , , 为 的中点, .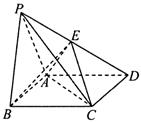 (1)、求证: 平面 ;(2)、求三棱锥 的体积.20. 已知 是焦距为 的椭圆 : 的右顶点,点 ,直线 交椭圆 于点 , 为线段 的中点.(1)、求椭圆 的方程;(2)、设过点 且斜率为 的直线 与椭圆 交于 、 两点,若 ,求直线 的斜率 .
(1)、求证: 平面 ;(2)、求三棱锥 的体积.20. 已知 是焦距为 的椭圆 : 的右顶点,点 ,直线 交椭圆 于点 , 为线段 的中点.(1)、求椭圆 的方程;(2)、设过点 且斜率为 的直线 与椭圆 交于 、 两点,若 ,求直线 的斜率 .