2017年江苏省苏州市吴中区中考数学一模试卷

试卷更新日期：2017-06-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 2的相反数是（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、2 D、 $\frac{1}{2}$

查看试题解析
2. 实数 $\sqrt{2}$ 的值在（）

A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间

查看试题解析
3. 年初，工信部官网发布了2016年通信运营业统计公报，数据显示，2016年，4G用户数呈爆发式增长，全年新增3.4亿户，总数达到770 000 000亿户，将770 000 000用科学记数法表示应为（）

A、0.77×10⁹ B、7.7×10⁷ C、7.7×10⁸ D、7.7×10⁹

查看试题解析
4. 把x²y﹣y分解因式，正确的是（）

A、y（x²﹣1） B、y（x+1） C、y（x﹣1） D、y（x+1）（x﹣1）

查看试题解析
5. 函数y= $\frac{1}{x + 2}$ 中，x的取值范围是（）

A、x≠0 B、x＞﹣2 C、x＜﹣2 D、x≠﹣2

查看试题解析
6. 一组数据：10，15，10，17，18，20．对于这组数据，下列说法错误的是（）

A、平均数是15 B、众数是10 C、中位数是17 D、方差是 $\frac{44}{3}$

查看试题解析
7.
如图，斜面AC的坡度（CD与AD的比）为1：2，AC=3 $\sqrt{5}$ 米，坡顶有旗杆BC，旗杆顶端B点与A点有一条彩带相连．若AB=10米，则旗杆BC的高度为（）

A、5米 B、6米 C、8米 D、（3+ $\sqrt{5}$ ）米

查看试题解析
8. 如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分面积为（结果保留π）（）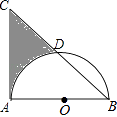

A、16 B、24﹣4π C、32﹣4π D、32﹣8π

查看试题解析
9. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列说法：
①2a+b=0；
②当﹣1≤x≤3时，y＜0；
③若（x₁ ， y₁）、（x₂ ， y₂）在函数图象上，当x₁＜x₂时，y₁＜y₂
④9a+3b+c=0
其中正确的是（）

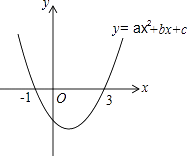A、①②④ B、①②③ C、①④ D、③④

查看试题解析
10. 如图，矩形ABCD中，AB= $\sqrt{3}$ ，BC= $\sqrt{6}$ ，点E在对角线BD上，且BE=1.8，连接AE并延长交DC于F，则 $\frac{C F}{C D}$ 等于（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{6}$

查看试题解析

二、填空题

11. 计算：a²•a³= ．

查看试题解析
12. 如图，直线l₁∥l₂ ，直线l₃与l₁、l₂分别交于A、B两点，若∠1=70°，则∠2= ．

查看试题解析
13. 某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图，则表示“无所谓”的家长人数为．

查看试题解析
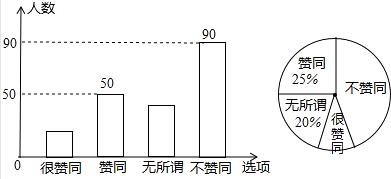14. 若2a﹣3b²=5，则6﹣2a+3b²= ．

查看试题解析
15. 如图，▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为．

查看试题解析
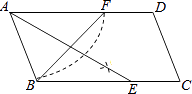16.
如图是一次函数y=kx+b的图象的大致位置，试判断关于x的一元二次方程x²﹣2x+kb+1=0的根的判别式△ 0（填：“＞”或“=”或“＜”）．

查看试题解析
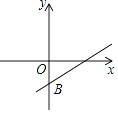17. 如图，二次函数Y=﹣ $\frac{1}{2}$ x²﹣ $\frac{3}{2}$ x+2象与x轴交于A、B两点，与y轴交于C点，点D（m，n）是抛物线在第二象限的部分上的一动点，则四边形OCDA的面积的最大值是．

查看试题解析
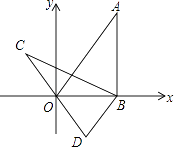
18.
如图，在平面直角坐标系xOy中，直线y= $\sqrt{3}$ x经过点A，作AB⊥x轴于点B，将△ABO绕点B逆时针旋转60°得到△CBD，若点B的坐标为（2，0），则点C的坐标为．

查看试题解析

三、解答题

19. 计算： $\sqrt{9}$ ﹣ ${(1 - \sqrt{2})}^{0}$ +|﹣5|．

查看试题解析
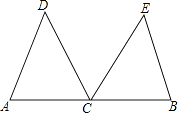
20. 解不等式组 ${\begin{matrix} 3 x - 3 \geq 2 x + 7 \\ \frac{2 x + 4}{3} < 3 - x \end{matrix}$ ．

查看试题解析
21. 先化简，再求值：（ $\frac{3}{x + 1}$ ﹣x+1）÷ $\frac{x^{2} + 4 x + 4}{x + 1}$ ，其中x= $\sqrt{2}$ ﹣2．

查看试题解析
22. 本学期开学前夕，苏州某文具店用4000元购进若干书包，很快售完，接着又用4500元购进第二批书包，已知第二批所购进书包的只数是第一批所购进书包的只数的1.5倍，且每只书包的进价比第一批的进价少5元，求第一批书包每只的进价是多少？

查看试题解析
23. 甲、乙两个不透明的口袋，甲口袋中装有3个分别标有数字1，2，3的小球，乙口袋中装有2个分别标有数字4，5的小球，它们的形状、大小完全相同，现随机从甲口袋中摸出一个小球记下数字，再从乙口袋中摸出一个小球记下数字．

(1)、请用列表或树状图的方法（只选其中一种），表示出两次所得数字可能出现的所有结果；

(2)、求出两个数字之积能被2整除的概率．

查看试题解析
24. 如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．

(1)、求证：△ACD≌△BCE；

(2)、若∠D=53°，求∠B的度数．

查看试题解析
25.
如图，一次函数y=﹣x+3的图象与反比例y= $\frac{k}{x}$ （k为常数，且k≠0）的图象交于A（1，a），B两点．

(1)、求反比例函数的表达式及点B的坐标；

(2)、在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．

查看试题解析
26. 如图，AB是⊙O的直径，BC是弦，过点O作OE⊥BC于H交⊙O于E，在OE的延长线上取一点D，使∠ODB=∠AEC，AE与BC交于F．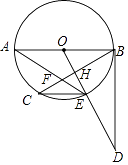

(1)、判断直线BD与⊙O的位置关系，并给出证明；

(2)、当⊙O的半径是5，BF=2 $\sqrt{11}$ ，EF= $\frac{11}{3}$ 时，求CE及BH的长．

查看试题解析
27.
如图，抛物线y=x²﹣bx+c过点B（3，0），C（0，﹣3），D为抛物线的顶点．

(1)、求抛物线的解析式以及顶点坐标；

(2)、点C关于抛物线y=x²﹣bx+c对称轴的对称点为E点，连接BC，BE，求∠CBE的正切值；

(3)、在（2）的条件下，点M是抛物线对称轴上且在CE上方的一点，是否存在点M使△DMB和△BCE相似？若存在，求点M坐标；若不存在，请说明理由．

查看试题解析
28. 如图，在矩形ABCD中，AB=6，BC=8，动点Q从点A出发，沿着AB方向以1个单位长度/秒的速度匀速运动，同时动点P从点B出发，沿着对角线BD方向也以1个单位长度/秒的速度匀速运动，设运动时间为t秒（0＜t≤5），以P为圆心，PB长为半径的⊙P与BD、AB的另一个交点分别为E、F，连结EF、QE．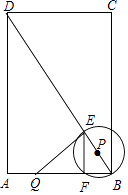

(1)、填空：FB=（用t的代数式表示）；

(2)、当t为何值时，点Q与点F相遇？

(3)、当线段QE与⊙P有两个公共点时，求t的取值范围．

查看试题解析