2017年江苏省南京市玄武区中考数学一模试卷

试卷更新日期：2017-06-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 计算1﹣（﹣2）²÷4的结果为（）

A、2 B、 $\frac{5}{4}$ C、0 D、﹣ $\frac{3}{4}$

查看试题解析
2. 南京规划地铁6号线由栖霞山站开往南京南站，全长32100米，这个数据用科学记数法表示为（）

A、321×10² B、32.1×10³ C、3.21×10⁴ D、3.21×10⁵

查看试题解析
3. 一元二次方程2x²+3x+1=0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定

查看试题解析
4. 下列运算结果正确的是（）

A、a²+a³=a⁵ B、a²•a³=a⁶ C、a³÷a²=a D、（a²）³=a⁵

查看试题解析
5. 如图，将矩形ABCD绕点A逆时针旋转90°至矩形AEFG，点D的旋转路径为 $\hat{D G}$ ，若AB=1，BC=2，则阴影部分的面积为（）

A、 $\frac{π}{3}$ + $\frac{\sqrt{3}}{2}$ B、1+ $\frac{\sqrt{3}}{2}$ C、 $\frac{π}{2}$ D、 $\frac{π}{3}$ +1

查看试题解析
6. 如图，将正六边形ABCDEF放入平面直角坐标系后，若点A、B、E的坐标分别为（a，b）、（3，1）、（﹣a，b），则点D的坐标为（）

A、（1，3） B、（3，﹣1） C、（﹣1，﹣3） D、（﹣3，1）

查看试题解析

二、填空题）

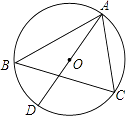
7. 分解因式：2x²+4x+2= ．

查看试题解析
8. 满足不等式组 ${\begin{matrix} x + 2 < 1 \\ 2 (x - 1) > - 8 \end{matrix}$ 的整数解为．

查看试题解析
9. 已知一组数据2，6，5，2，4，则这组数据的中位数是．

查看试题解析
10. 计算 $\frac{\sqrt{12} - 3}{\sqrt{3}}$ = ．

查看试题解析
11. 若关于x的方程x²+mx+5=0有一个根为1，则该方程的另一根为．

查看试题解析
12. 如图，△ABC是⊙O的内接三角形，AD是⊙O的直径，∠ABC=50°，则∠CAD= ．

查看试题解析
13. 如图，在▱ABCD中，E、F分别是AD、CD的中点，EF与BD相交于点M，若△DEM的面积为1，则▱ABCD的面积为．

查看试题解析
14. 如图，A（a，b）、B（1，4）（a＞1）是反比例函数y= $\frac{k}{x}$ （x＞0）图象上两点，过A、B分别作x轴、y轴的垂线，垂足分别为C、D、E、F，AE、BD交于点G．则四边形ACDG的面积随着a的增大而．（填“减小”、“不变”或“增大”）

查看试题解析
15. 二次函数y=a（x﹣b）²+c（a＜0）的图象经过点（1，1）和（3，3），则b的取值范围是．

查看试题解析
16. 如图，在△ABC中，∠C=90°，AC=BC=1，P为△ABC内一个动点，∠PAB=∠PBC，则CP的最小值为．

查看试题解析

三、解答题

17. 解方程

(1)、解方程组 ${\begin{matrix} x + 2 y = 3 \\ 2 x - y = 1 \end{matrix}$

(2)、解方程 $\frac{1}{x - 1}$ = $\frac{2}{x + 3}$ ．

查看试题解析
18. 计算 $\frac{x}{x^{2} - 1}$ ÷（1+ $\frac{1}{x - 1}$ ）．

查看试题解析
19. 一个不透明的袋子中，装有2个红球，1个白球，1个黄球，这些球除颜色外都相同．求下列事件的概率：

(1)、搅匀后从中任意摸出1个球，恰好是红球；

(2)、搅匀后从中任意摸出2个球，2个都是红球．

查看试题解析
20. 某公司在某市五个区投放共享单车供市民使用，投放量的分布及投放后的使用情况统计如下．

(1)、该公司在全市一共投放了万辆共享单车；

(2)、在扇形统计图中，B区所对应扇形的圆心角为°；

(3)、该公司在全市投放的共享单车的使用量占投放量的85%，请计算C区共享单车的使用量并补全条形统计图．

查看试题解析
21. 如图，在▱ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．

(1)、求证：△AEH≌△CGF；

(2)、求证：四边形EFGH是菱形．

查看试题解析
22.
用两种方法证明“直角三角形斜边上的中线等于斜边的一半”．
已知：如图1，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线．
求证：CD= $\frac{1}{2}$ AB．

证法1：如图2，在∠ACB的内部作∠BCE=∠B，
CE与AB相交于点E．
∵∠BCE=∠B，
∴ ．
∵∠BCE+∠ACE=90°，
∴∠B+∠ACE=90°．
又∵ ，
∴∠ACE=∠A．
∴EA=EC．
∴EA=EB=EC，
即CE是斜边AB上的中线，且CE= $\frac{1}{2}$ AB．
又∵CD是斜边AB上的中线，即CD与CE重合，
∴CD= $\frac{1}{2}$ AB．
请把证法1补充完整，并用不同的方法完成证法2．

查看试题解析
23. 同时点燃甲乙两根蜡烛，蜡烛燃烧剩下的长度y（cm）与燃烧时间x（min）的关系如图所示．

(1)、求乙蜡烛剩下的长度y与燃烧时间x的函数表达式；

(2)、求点P的坐标，并说明其实际意义；

(3)、求点燃多长时间，甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍．

查看试题解析
24. 定义：在△ABC中，∠C=30°，我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦，记作thi A，即thi A= $\frac{∠ A 的对边}{∠ C 的对边}$ = $\frac{B C}{A B}$ ．请解答下列问题：
已知：在△ABC中，∠C=30°．

(1)、若∠A=45°，求thi A的值；

(2)、若thi A= $\sqrt{3}$ ，则∠A=°；

(3)、若∠A是锐角，探究thi A与sinA的数量关系．

查看试题解析
25. A厂一月份产值为16万元，因管理不善，二、三月份产值的月平均下降率为x（0＜x＜1）．B厂一月份产值为12万元，二月份产值下降率为x，经过技术革新，三月份产值增长，增长率为2x．三月份A、B两厂产值分别为y_A、y_B（单位：万元）．

(1)、分别写出y_A、y_B与x的函数表达式；

(2)、当y_A=y_B时，求x的值；

(3)、当x为何值时，三月份A、B两厂产值的差距最大？最大值是多少万元？

查看试题解析
26. 如图，在Rt△ABC中，∠A=90°，点D、E分别在AC、BC上，且CD•BC=AC•CE，以E为圆心，DE长为半径作圆，⊙E经过点B，与AB、BC分别交于点F、G．

(1)、求证：AC是⊙E的切线．

(2)、若AF=4，CG=5，求⊙E的半径；

(3)、若Rt△ABC的内切圆圆心为I，则IE= ．

查看试题解析
27.
在△ABC中，D为BC边上一点．

(1)、如图①，在Rt△ABC中，∠C=90°，将△ABC沿着AD折叠，点C落在AB边上．请用直尺和圆规作出点D（不写作法，保留作图痕迹）；

(2)、如图②，将△ABC沿着过点D的直线折叠，点C落在AB边上的E处．
①若DE⊥AB，垂足为E，请用直尺和圆规作出点D（不写作法，保留作图痕迹）；
②若AB=4 $\sqrt{2}$ ，BC=6，∠B=45°，则CD的取值范围是．

查看试题解析