2017年江苏省南京市秦淮区中考数学一模试卷

试卷更新日期：2017-06-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列四个数中，是负数的是（）

A、|﹣3| B、（﹣3）² C、﹣（﹣3） D、﹣3²

查看试题解析
2. 据南京市统计局调查数据显示，截至2016年年底，全市汽车拥有量首次进入全国“200万俱乐部”，达到了2 217 000辆．将2 217 000用科学记数法表示是（）

A、0.2217×10⁶ B、0.2217×10⁷ C、2.217×10⁶ D、2.217×10⁷

查看试题解析
3. 如图，数轴上的点A表示的数可能是下列各数中的（）

A、﹣8的算术平方根 B、10的负的平方根 C、﹣10的算术平方根 D、﹣65的立方根

查看试题解析
4. 某公司的拓展部有五个员工，他们每月的工资分别是3000元，5000元，7000元，4000元和10000元，那么他们工资的中位数为（）

A、4000元 B、5000元 C、7000元 D、10000元

查看试题解析
5. 下列长度的三条线段能组成锐角三角形的是（）

A、2，3，3 B、2，3，4 C、2，3，5 D、3，4，5

查看试题解析
6. 如图，将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上，恰好完全重合，BE、CE分别交AD于点F、G，BC=6，AF：FG：GD=3：2：1，则AB的长为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析

二、填空题

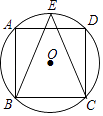
7. ﹣2的倒数是；﹣2的相反数是．

查看试题解析
8. 若式子 $\sqrt{x + 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
9. 计算 $\frac{\sqrt{5} \times \sqrt{12}}{\sqrt{3}}$ 的结果是．

查看试题解析
10. 方程 $\frac{1}{x - 2} = \frac{3}{x}$ 的根是．

查看试题解析
11. 正方形ABCD内接于⊙O，E是 $\hat{A D}$ 的中点，连接BE、CE，则∠ABE=°．

查看试题解析
12. 如图，将△ABC绕点B顺时针旋转到△DBE的位置．连接AD，若∠ADB=60°，则∠1=°．

查看试题解析
13. 已知二次函数y=ax²+bx+c的部分图象如图所示，则关于x的方程ax²+bx+c=0的两个根的和为．

查看试题解析
14. 某种商品因换季准备打折出售，如果按定价的七五折出售将赔25元，而按定价的九折出售将赚20元，则商品的定价是元．

查看试题解析
15. 我们已经学习过反比例函数y= $\frac{1}{x}$ 的图象和性质，请回顾研究它的过程，对函数y= $\frac{1}{x^{2}}$ 进行探索．下列结论：

①图象在第一、二象限，②图象在第一、三象限，
③图象关于y轴对称，④图象关于原点对称，
⑤当x＞0时，y随x增大而增大；当x＜0时，y随x增大而增大，
⑥当x＞0时，y随x增大而减小；当x＜0时，y随x增大而增大，
是函数y= $\frac{1}{x^{2}}$ 的性质及它的图象特征的是：．（填写所有正确答案的序号）

查看试题解析
16. 如图，在△ABC中，∠C=90°，CA=4，CB=3. $\hat{G H}$ 与CA延长线、AB、CB延长线相切，切点分别为E、D、F，则该弧所在圆的半径为．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{matrix} 2 + 3 (x - 3) \geq 5 \\ \frac{1 + 2 x}{3} > x - 2. \end{matrix}$ ．

查看试题解析
18. 化简 $\frac{2}{x^{2} - 4}$ ﹣ $\frac{1}{2 x - 4}$ ．

查看试题解析
19. 如图，在Rt△ABC中，∠ACB=90°，D、E分别是AB、AC的中点，连接DE并延长至点F，使EF=DE，连接AF、DC．求证：四边形ADCF是菱形．

查看试题解析
20. 脸谱是中国戏曲男演员脸部的彩色化妆．这种脸部化妆主要用于净（花脸）和丑（小丑），表现人物的性格和特征．现有四张脸谱，如图所示：有两张相同的表现忠勇侠义的净角姜维，有一张表现直爽刚毅的净角包拯，有一张表现阴险奸诈的丑角夏侯婴．

(1)、随机抽取一张，获得一张净角脸谱的概率是；

(2)、随机抽取两张，求获得一张姜维脸谱和一张包拯脸谱的概率．

查看试题解析
21. 已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如下表：
x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…

(1)、求该函数的表达式；

(2)、当y＜5时，x的取值范围是．

查看试题解析
22. “智慧南京、绿色出行”，骑共享单车出行已经成为一种时尚．记者随机调查了一些骑共享单车的秦淮区市民，并将他们对各种品牌单车的选择情况绘制成图①和图②的统计图（A：摩拜单车；B：ofo单车；C：HelloBike）．请根据图中提供的信息，解答下列问题：

(1)、在图①中，C部分所占扇形的圆心角度数为°；

(2)、将图②补充完整；

(3)、根据抽样调查结果，请你估计某天该区48万名骑共享单车的市民中有多少名选择摩拜单车？

查看试题解析
23. 某商场以80元/个的价格购进1000个保温杯．经市场调研，保温杯定价为100元/个时可全部售完，定价每提高1元，销售量将减少5个．未卖完的保温杯可以直接退还厂家．要使商场利润达到60500元，保温杯的定价应为多少元？

查看试题解析
24.
如图，在路边安装路灯，灯柱BC高15m，与灯杆AB的夹角ABC为120°．路灯采用锥形灯罩，照射范围DE长为18.9m，从D、E两处测得路灯A的仰角分别为∠ADE=80.5°，∠AED=45°．求灯杆AB的长度．（参考数据：cos80.5°≈0.2，tan80.5°≈6.0）

查看试题解析
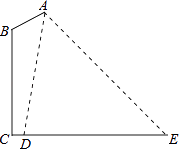25. 如图，在△ABC中，AB=AC，以AB为直径作半圆O交BC于点D，过点D作DE⊥AC，垂足为E．

(1)、求证：DE是⊙O的切线；

(2)、若CE=1，BC=6，求半圆O的半径的长．

查看试题解析

26. 一组对边平行，另一组对边相等且不平行的四边形叫做等腰梯形．

(1)、类比研究

我们在学完平行四边形后，知道可以从对称性、边、角和对角线四个角度对四边形进行研究，完成表．

四边形

对称性

边

角

对角线

平行

四边形

．

两组对边分别平行，两组对边分别相等．

两组对角

分别相等．

对角线互相平分．

等腰

梯形

轴对称图形，过平行的一组对边中点的直线是它的对称轴．

一组对边平行，另一组对边相等．

．

(2)、

演绎论证

证明等腰梯形有关角和对角线的性质．

已知：在等腰梯形ABCD中，AD∥BC，AB=DC，AC、BD是对角线．

求证：

证明：

揭示关系

我们可以用图来揭示三角形和一些特殊三角形之间的关系．

(3)、请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系．

查看试题解析

27. 一列快车和一列慢车同时从甲地出发，分别以速度v₁、v₂（单位：km/h，且v₁＞2v₂）匀速驶向乙地．快车到达乙地后停留了2h，沿原路仍以速度v₁匀速返回甲地．设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示从慢车出发至慢车到达乙地的过程中，y与x之间的函数关系．根据图象进行以下探究：

(1)、甲、乙两地之间的距离为 km；

(2)、求线段AB、CD所表示的y与x之间的函数表达式；

(3)、慢车出发多长时间后，两车相距480km？

查看试题解析

x	…	﹣1	0	1	2	3	…
y	…	10	5	2	1	2	…