2017年河南省周口市西华县中考数学二模试卷
试卷更新日期:2017-06-22 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的数是( )A、 B、 C、 D、2. 据报道,中国工商银行2015年实现净利润2 777亿元.数据2 777亿用科学记数法表示为( )A、2.777×1010 B、2.777×1011 C、2.777×1012 D、0.2777×10133. 下列计算正确的是( )A、 B、(﹣3)2=6 C、3a4﹣2a2=a2 D、(﹣a3)2=a54. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 某班50名同学的年龄统计如下:
5. 某班50名同学的年龄统计如下:年龄(岁)
12
13
14
15
学生数(人)
1
23
20
6
该班同学年龄的众数和中位数分别是( )
A、6,13 B、13,13.5 C、13,14 D、14,146. 如图,AB∥CD,AD与BC相交于点O,若AO=2,DO=4,BO=3,则BC的长为( ) A、6 B、9 C、12 D、157. 如图所示,点D是弦AB的中点,点C在⊙O上,CD经过圆心O,则下列结论中不一定正确的是( )
A、6 B、9 C、12 D、157. 如图所示,点D是弦AB的中点,点C在⊙O上,CD经过圆心O,则下列结论中不一定正确的是( ) A、CD⊥AB B、∠OAD=2∠CBD C、∠AOD=2∠BCD D、弧AC=弧BC8. 从2,2,3,4四个数中随机取两个数,第一个作为个位上的数字,第二个作为十位上的数字,组成一个两位数,则这个两位数是2的倍数的概率是( )A、1 B、 C、 D、9. 如图,CB平分∠ECD,AB∥CD,AB与EC交于点A.若∠B=40°,则∠EAB的度数为( )
A、CD⊥AB B、∠OAD=2∠CBD C、∠AOD=2∠BCD D、弧AC=弧BC8. 从2,2,3,4四个数中随机取两个数,第一个作为个位上的数字,第二个作为十位上的数字,组成一个两位数,则这个两位数是2的倍数的概率是( )A、1 B、 C、 D、9. 如图,CB平分∠ECD,AB∥CD,AB与EC交于点A.若∠B=40°,则∠EAB的度数为( ) A、50° B、60° C、70° D、80°10. 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )
A、50° B、60° C、70° D、80°10. 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )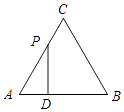 A、
A、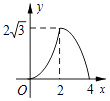 B、
B、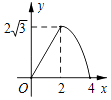 C、
C、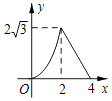 D、
D、
二、填空题
-
11. 计算: ﹣|﹣2|= .12. 如图,矩形ABCD中,AB=2cm,BC=6cm,把△ABC沿对角线AC折叠,得到△AB′C,且B′C与AD相交于点E,则AE的长为cm.
 13. 如图,Rt△ABC中,∠B=90°,AB=6,BC=8,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A′B′C,则边AB扫过的面积(图中阴影部分)是 .
13. 如图,Rt△ABC中,∠B=90°,AB=6,BC=8,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A′B′C,则边AB扫过的面积(图中阴影部分)是 . 14. 已知y=﹣ x2﹣3x+4(﹣10≤x≤0)的图象上有一动点P,点P的纵坐标为整数值时,记为“好点”,则有多个“好点”,其“好点”的个数为 .15. 如图,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为 .
14. 已知y=﹣ x2﹣3x+4(﹣10≤x≤0)的图象上有一动点P,点P的纵坐标为整数值时,记为“好点”,则有多个“好点”,其“好点”的个数为 .15. 如图,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为 .
三、解答题
-
16. 先化简,再求值:(a+ )÷(a﹣2+ ),请从﹣1,0,1中选取一个作为a的值代入求值.17. 如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
 (1)、求证:AP是⊙O的切线;(2)、求PD的长.18. 2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年,9月3日全国各地将举行有关纪念活动.为了解初中学生对二战历史的知晓情况,某初中课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A、B、C、D四类,其中A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”;D类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②):
(1)、求证:AP是⊙O的切线;(2)、求PD的长.18. 2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年,9月3日全国各地将举行有关纪念活动.为了解初中学生对二战历史的知晓情况,某初中课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A、B、C、D四类,其中A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”;D类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②): (1)、在这次抽样调查中,一共抽查了名学生;(2)、请把图①中的条形统计图补充完整;(3)、图②的扇形统计图中D类部分所对应扇形的圆心角的度数为;(4)、如果这所学校共有初中学生1500名,请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名?19. 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
(1)、在这次抽样调查中,一共抽查了名学生;(2)、请把图①中的条形统计图补充完整;(3)、图②的扇形统计图中D类部分所对应扇形的圆心角的度数为;(4)、如果这所学校共有初中学生1500名,请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名?19. 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86) 20. 如图,已知矩形OABC中,OA=3,AB=4,双曲线y= (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
20. 如图,已知矩形OABC中,OA=3,AB=4,双曲线y= (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD (1)、求k的值和点E的坐标;(2)、点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.21. “五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.(1)、求在甲商店购物时y与x之间的函数关系;(2)、两种购物方式对应的函数图象如图所示,求交点C的坐标;(3)、根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
(1)、求k的值和点E的坐标;(2)、点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.21. “五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.(1)、求在甲商店购物时y与x之间的函数关系;(2)、两种购物方式对应的函数图象如图所示,求交点C的坐标;(3)、根据图象,请直接写出“五一”期间选择哪家商店购物更优惠. 22. 问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求 的值.(1)、初步尝试
22. 问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求 的值.(1)、初步尝试如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得 的值为 .
 (2)、类比探究
(2)、类比探究如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 :1,求 的值.
 (3)、延伸拓展
(3)、延伸拓展如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 =m,且点D、E的运动速度相等,试用含m的代数式表示 的值(直接写出果,不必写解答过程).
 23. 如图,抛物线y=ax2+bx﹣3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=﹣1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).
23. 如图,抛物线y=ax2+bx﹣3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=﹣1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合). (1)、直接写出抛物线的解析式;(2)、小唐探究点P的位置时发现:当动点N在对称轴l上时,存在PB⊥NB,且PB=NB的关系,请求出点P的坐标;(3)、是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值;若不存在,请说明理由.
(1)、直接写出抛物线的解析式;(2)、小唐探究点P的位置时发现:当动点N在对称轴l上时,存在PB⊥NB,且PB=NB的关系,请求出点P的坐标;(3)、是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值;若不存在,请说明理由.