2017年河南省天宏大联考中考数学一模试卷
试卷更新日期:2017-06-22 类型:中考模拟
一、选择题
-
1. 在数﹣3,﹣2,0,3中,大小在﹣1和2之间的数是( )A、﹣3 B、﹣2 C、0 D、32. 某同学画出了如图所示的几何体的三种视图,其中正确的是( )

A、①② B、①③ C、②③ D、②3. 微信更具移动ID所带来的数据,发布了“微信用户春节迁徙数据报告”,该报告显示,2016年1月24日春运至2月4日期间,人口流入最多的省份是河南,作为劳务输出大省,河南约有313万微信用户在春节期间返乡,313万用科学记数法表示为( )A、3.13×105 B、3.13×106 C、3.13×102 D、313×1044. 如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( ) A、4 B、7 C、3 D、125. 已知,一次函数y1=ax+b与反比例函数y2= 的图象如图所示,当y1<y2时,x的取值范围是( )
A、4 B、7 C、3 D、125. 已知,一次函数y1=ax+b与反比例函数y2= 的图象如图所示,当y1<y2时,x的取值范围是( ) A、x<2 B、0<x<2或x>5 C、2<r<5 D、r>56. 已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
A、x<2 B、0<x<2或x>5 C、2<r<5 D、r>56. 已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )①m是无理数;
②m是方程m2﹣12=0的解;
③m满足不等式组 ;
④m是12的算术平方根.
A、①② B、①③ C、③ D、①②④7.如图,挂在弹簧称上的长方体铁块浸没在水中,提着弹簧称匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧称的读数F(N)与时间t(s)的函数图象大致是( )
 A、
A、 B、
B、 C、
C、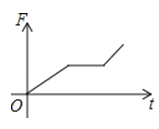 D、
D、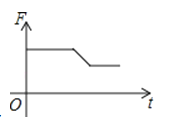 8. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
8. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) A、2 B、 C、 D、9. 将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )
A、2 B、 C、 D、9. 将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )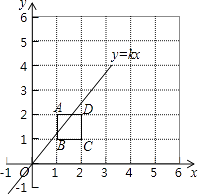 A、3 B、2 C、1 D、10. 在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( )
A、3 B、2 C、1 D、10. 在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( ) A、( )2016 B、( )2017 C、( )2016 D、( )2017
A、( )2016 B、( )2017 C、( )2016 D、( )2017二、填空题
-
11. |﹣2|﹣(π﹣3)0= .12. 用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为度.
 13. 一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是 .
13. 一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是 .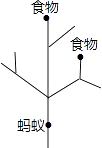 14. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .
14. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .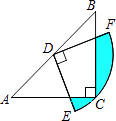 15. 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为 .
15. 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为 .
三、解答题
-
16. 先化简,再求值: ÷ ,其中m是方程x2+2x﹣3=0的根.17. 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
20
0.10
70≤x<80
30
b
80≤x<90
a
0.30
90≤x≤100
80
0.40
请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、这次比赛成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人? 18. 在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.(1)、求证:BF⊥AF;(2)、当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明.
18. 在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.(1)、求证:BF⊥AF;(2)、当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明. 19. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
19. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 20. 某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示;
20. 某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示; (1)、求y(千克)与销售价x的函数关系式;(2)、该经销商想要获得150元的销售利润,销售价应定为多少?21. 有这样一个问题:探究函数 的图象与性质.小怀根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:(1)、函数 的自变量x的取值范围是;(2)、列出y与x的几组对应值.请直接写出m的值,m=;(3)、请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;(4)、结合函数的图象,写出函数 的一条性质.
(1)、求y(千克)与销售价x的函数关系式;(2)、该经销商想要获得150元的销售利润,销售价应定为多少?21. 有这样一个问题:探究函数 的图象与性质.小怀根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:(1)、函数 的自变量x的取值范围是;(2)、列出y与x的几组对应值.请直接写出m的值,m=;(3)、请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;(4)、结合函数的图象,写出函数 的一条性质.x
…
﹣5
﹣4
﹣3
﹣2
﹣
﹣
0
1
2
m
4
5
…
y
…
2
3
﹣1
0
…
22. 我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c. (1)、【特例探索】
(1)、【特例探索】如图1,当∠ABE=45°,c=2 时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
(2)、【归纳证明】请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
(3)、【拓展应用】如图4,在▱ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ,AB=3.求AF的长.
 23. 如图,抛物线y= x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).
23. 如图,抛物线y= x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0). (1)、求抛物线的解析式;(2)、若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;(3)、在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标.
(1)、求抛物线的解析式;(2)、若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;(3)、在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标.