2016-2017学年山东省烟台市高一下学期期中数学试卷

试卷更新日期：2017-06-22 类型：期中考试

进入出卷网下载

一、选择题

1. 某校高一年级举办歌咏比赛，7位裁判为某班级打出的分数如图茎叶图所示，左边数字表示十位数字，右边数字表示个位数字，则这些数据的中位数是（）

A、84 B、85 C、88 D、89

查看试题解析
2. 已知圆x²+y²+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是（）

A、﹣2 B、﹣4 C、﹣6 D、﹣8

查看试题解析
3. 观察下列散点图，其中两个变量的相关关系判断正确的是（）

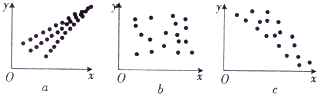A、a为正相关，b为负相关，c为不相关 B、a为负相关，b为不相关，c为正相关 C、a为负相关，b为正相关，c为不相关 D、a为正相关，b为不相关，c为负相关

查看试题解析
4. 如图是总体密度曲线，下列说法正确的是（）

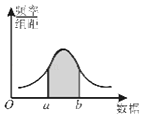A、组距越大，频率分布折线图越接近于它 B、样本容量越小，频率分布折线图越接近于它 C、阴影部分的面积代表总体在（a，b）内取值的百分比 D、阴影部分的平均高度代表总体在（a，b）内取值的百分比

查看试题解析
5. 圆（x﹣3）²+（y﹣3）²=4上到直线3x+4y﹣16=0的距离等于1的点有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. “勾股定理”在西方被称为“毕达哥拉斯定理”，三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”，用数形结合的方法给出了勾股定理的详细证明．如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角 $a = \frac{π}{6}$ ，现在向该正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内的概率是（）

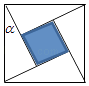A、 $1 - \frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{4 - \sqrt{3}}{4}$ D、 $\frac{\sqrt{3}}{4}$

查看试题解析
7. 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a=（）

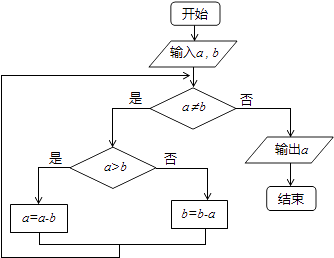A、0 B、2 C、4 D、14

查看试题解析
8. 袋中装有红球3个、白球2个、黑球1个，从中任取2个，则互斥而不对立的两个事件是（）

A、至少有一个白球；至少有一个红球 B、至少有一个白球；红、黑球各一个 C、恰有一个白球；一个白球一个黑球 D、至少有一个白球；都是白球

查看试题解析
9. 以（a，1）为圆心，且与两直线x﹣y+1=0及x﹣y﹣3=0同时相切的圆的标准方程为（）

A、x²+（y﹣1）²=2 B、（x﹣2）²+（y﹣1）²=2 C、x²+（y﹣1）²=8 D、（x﹣2）²+（y﹣1）²=8

查看试题解析
10. 一名射击运动员射击10次，命中环数如下，则该运动员命中环数的标准差为（）
10 10 10 9 10 8 8 10 10 8．

A、0.81 B、0.9 C、0.64 D、0.8

查看试题解析
11. 现有1名女教师和2名男教师参加说题比赛，共有2道备选题目，若每位选手从中有放回地随机选出一道题进行说题，其中恰有一男一女抽到同一道题的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
12. 若圆C：x²+y²+2x﹣4y+3=0关于直线2ax+by+6=0对称，则由点（a，b）向圆C所作切线长的最小值是（　　）

A、2 B、3 C、4 D、6

查看试题解析

二、填空题

13. 某班级有50名学生，现要采取系统抽样的方法在这50名学生中抽出10名学生，将这50名学生随机编号1﹣50号，并分组，第一组1﹣5号，第二组6﹣10号，…，第十组45﹣50号，若在第三组中抽得号码为12的学生，则在第八组中抽得号码为的学生．

查看试题解析
14. 执行如图所示的程序框图，输出的S值为

查看试题解析
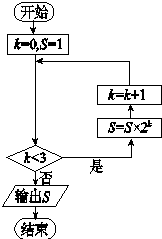15. 从一副扑克牌中取出1张A，2张K，2张Q放入一盒子中，然后从这5张牌中随机取出两张，则这两张牌大小不同的概率为．

查看试题解析
16. 在平面直角坐标系xOy中，已知直线y=x+2与x轴、y轴分别交于M、N两点，点P在圆（x﹣a）²+y²=2（a＞0）上运动，若∠MPN恒为锐角，则实数a的取值范围是．

查看试题解析

三、解答题

17. 某地最近十年对某商品的需求量逐年上升，下表是部分统计数据：
年份
2008
2010
2012
2014
2016
需要量（万件）
236
246
257
276
286

(1)、利用所给数据求年需求量y与年份x之间的回归直线方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ ；

(2)、预测该地2018年的商品需求量（结果保留整数）．

查看试题解析
18. 在△ABC中，已知|BC|=4，且 $\frac{| A B |}{| A C |} = λ$ ，求点A的轨迹方程，并说明轨迹是什么图形．

查看试题解析
19. 已知正方形ABCD的边长为1，弧BD是以点A为圆心的圆弧．

(1)、在正方形内任取一点M，求事件“|AM|≤1”的概率；

(2)、用大豆将正方形均匀铺满，经清点，发现大豆一共28粒，其中有22粒落在圆中阴影部分内，请据此估计圆周率π的近似值（精确到0.01）．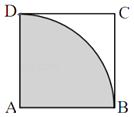

查看试题解析
20. 已知直线l：（k﹣1）x﹣2y+5﹣3k=0（k∈R）恒过定点P，圆C经过点A（4，0）和点P，且圆心在直线x﹣2y+1=0上．

(1)、求定点P的坐标；

(2)、求圆C的方程；

(3)、已知点P为圆C直径的一个端点，若另一个端点为点Q，问：在y轴上是否存在一点M（0，m），使得△PMQ为直角三角形，若存在，求出m的值，若不存在，请说明理由．

查看试题解析
21. 从某小区随机抽取40个家庭，收集了这40个家庭去年的月均用水量（单位：吨）的数据，整理得到频数分布表和频率分布直方图．
分组
频数
[2，4）
2
[4，6）
10
[6，8）
16
[8，10）
8
[10，12]
4
合计
40

(1)、求频率分布直方图中a，b的值；

(2)、从该小区随机选取一个家庭，试估计这个家庭去年的月均用水量不低于6吨的概率；

(3)、在这40个家庭中，用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本，将该样本看成一个总体，从中任意选取2个家庭，求其中恰有一个家庭的月均用水量不低于8吨的概率．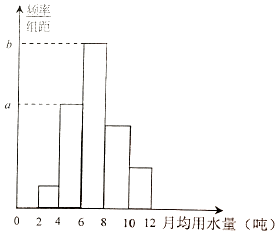

查看试题解析
22. 已知圆M：x²+（y﹣2）²=r²（r＞0）与曲线C：（y﹣2）（3x﹣4y+3）=0有三个不同的交点．

(1)、求圆M的方程；

(2)、已知点Q是x轴上的动点，QA，QB分别切圆M于A，B两点．
①若 $| A B | = \frac{4 \sqrt{2}}{3}$ ，求|MQ|及直线MQ的方程；
②求证：直线AB恒过定点．

查看试题解析

年份	2008	2010	2012	2014	2016
需要量（万件）	236	246	257	276	286

分组	频数
[2，4）	2
[4，6）	10
[6，8）	16
[8，10）	8
[10，12]	4
合计	40