2016-2017学年山东省德州市武城二中高一下学期期中数学试卷

试卷更新日期：2017-06-22 类型：期中考试

进入出卷网下载

一、单选题

1. 向量 $(\vec{A B} + \vec{M B}) + (\vec{B O} + \vec{B C}) + \vec{O M}$ 化简后等于（）

A、 $\vec{B C}$ B、 $\vec{A B}$ C、 $\vec{A C}$ D、 $\vec{A M}$

查看试题解析
2. 设向量 $a = (\cos 45^{\circ} ， \sin 45^{\circ}) ， b = (\cos 15^{\circ} ， \sin 15^{\circ}) ， a \cdot b$ =（）

A、- $\frac{\sqrt{3}}{2}$ B、- $\frac{1}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
3. 已知 $\vec{a} ， \vec{b}$ 均为单位向量，并且它们的夹角为120°，那么 $| \vec{a} - 2 \vec{b} |$ 等于（）

A、 $\sqrt{3}$ B、 $\sqrt{7}$ C、3 D、7

查看试题解析
4. 已知平面向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ ， $\vec{a}$ =（﹣1，1）， $\vec{b}$ =（2，3）， $\vec{c}$ =（﹣2，k），若（ $\vec{a}$ + $\vec{b}$ ）∥ $\vec{c}$ ，则实数k=（）

A、4 B、﹣4 C、8 D、﹣8

查看试题解析
5. 在△ABC中， $a = 2 ， b = 4 ， c = 30^{\circ} ，则 \vec{B C} \cdot \vec{C A}$ =（）

A、 $4 \sqrt{3}$ B、4 C、﹣ $4 \sqrt{3}$ D、﹣4

查看试题解析
6. 若cosθ＜0，且sin2θ＜0，则角θ的终边所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. $\sqrt{1 + \sin 6} + \sqrt{1 - \sin 6}$
=（）

A、2sin3 B、﹣2sin3 C、2cos3 D、﹣2cos3

查看试题解析
8. 函数 $f (x) = \sin^{2} (x + \frac{π}{4}) + \cos^{2} (x - \frac{π}{4}) - 1$ 是（）

A、周期为π的奇函数 B、周期为π的偶函数 C、周期为2π的奇函数 D、周期为2π的偶函数

查看试题解析
9. 在△ABC中，设 $\vec{A B} = \vec{a} ， \vec{A C} = \vec{b}$ ，若点D满足 $\vec{B D} = 2 \vec{D C}$ ，则 $\vec{A D}$ =（）

A、 $\frac{1}{3} \vec{a} + \frac{2}{3} \vec{b}$ B、 $\frac{5}{3} \vec{a} - \frac{2}{3} \vec{b}$ C、﹣ $\frac{1}{3} \vec{a} + \frac{2}{3} \vec{b}$ D、 $\frac{2}{3} \vec{a} + \frac{1}{3} \vec{b}$

查看试题解析
10. 已知 $\tan (α + β) = \frac{2}{5} ， \tan (β - \frac{π}{4}) = \frac{1}{4}$ ，则 $\frac{1 + \tan α}{1 - \tan α}$ 等于（）

A、 $\frac{1}{6}$ B、 $\frac{13}{18}$ C、 $\frac{13}{22}$ D、 $\frac{3}{22}$

查看试题解析
11. 要得到函数 $y = \cos (2 x - \frac{π}{3})$ 的图象，只需将函数y=sin2x的图象（）

A、向左平移 $\frac{π}{12}$ 个单位 B、向右平移 $\frac{π}{12}$ 个单位 C、向左平移 $\frac{π}{6}$ 个单位 D、向右平移 $\frac{π}{6}$ 个单位

查看试题解析
12. 已知 $3 \vec{a} + 4 \vec{b} + 5 \vec{c} = 0 ，且 | \vec{a} | = | \vec{b} | = | \vec{c} | = 1$ ，则 $\vec{b} \cdot (\vec{a} + \vec{c})$ 等于（）

A、﹣ $\frac{4}{5}$ B、﹣ $\frac{3}{5}$ C、0 D、 $\frac{3}{5}$

查看试题解析

二、填空题

13. 已知 $| \vec{a} | =5 ， | \vec{b} | = 3 ，且 \vec{a} \cdot \vec{b} =- 9 ，则 \vec{a}$ 在 $\vec{b}$ 上的射影的数量为．

查看试题解析
14. 设向量 $\vec{a} = (1 ， 2) ， \vec{b} = (2 ， 3)$ ，若向量 $λ \vec{a} + \vec{b}$ 与向量 $\vec{c} = (- 4 ， 6)$ 垂直，则λ= ．

查看试题解析
15. 已知 $\sin α = \frac{24}{25} ，且 π < α < \frac{5 π}{4}$ ，则cosα﹣sinα= ．

查看试题解析
16. 给出下列命题：
①函数 $y = 2 \cos^{2} (\frac{1}{3} x + \frac{π}{4}) - 1$ 是奇函数；
②存在实数α，使得sinα+cosα= $\frac{3}{2}$ ；
③若α，β是第一象限角且α＜β，则tanα＜tanβ；
④ $x = \frac{π}{8}$ 是函数 $y = \sin (2 x + \frac{5 π}{4})$ 的一条对称轴方程；
⑤函数 $y = \sin (2 x + \frac{π}{3})$ 的图象关于点 $(\frac{π}{12} ， 0)$ 成中心对称图形．
其中命题正确的是（填序号）．

查看试题解析

三、解答题

17. 设两个非零向量 $\vec{a}$ 与 $\vec{b}$ 不共线．

(1)、若 $\vec{A B}$ = $\vec{a}$ + $\vec{b}$ ， $\vec{B C}$ =2 $\vec{a}$ +8 $\vec{b}$ ， $\vec{C D}$ =3（ $\vec{a}$ ﹣ $\vec{b}$ ）．求证：A，B，D三点共线；

(2)、试确定实数k，使k $\vec{a}$ + $\vec{b}$ 和 $\vec{a}$ +k $\vec{b}$ 共线．

查看试题解析
18. 已知 $\frac{π}{4} < α < \frac{3 π}{4} ， 0 < β < \frac{π}{4} ， \cos (\frac{π}{4} + α) = - \frac{4}{5} ， \sin (\frac{3 π}{4} + β) = \frac{12}{13}$ ．

(1)、求sin（α+β）的值；

(2)、求cos（α﹣β）的值．

查看试题解析
19. 设平面向量 $\vec{a}$ =（cosx，sinx）， $\vec{b}$ =（cosx+2 $\sqrt{3}$ ，sinx）， $\vec{c}$ =（sinα，cosα），x∈R．

(1)、若 $\vec{a} ⊥ \vec{c}$ ，求cos（2x+2α）的值；

(2)、若α=0，求函数f（x）= $\vec{a} \cdot (\vec{b} - 2 \vec{c})$ 的最大值，并求出相应的x值．

查看试题解析
20. 已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜ $\frac{π}{2}$ ）的部分图象如图所示．

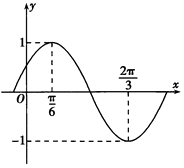(1)、求函数f（x）的解析式，并写出f（x）的单调减区间；

(2)、已知△ABC的内角分别是A，B，C，A为锐角，且f $(\frac{A}{2} - \frac{π}{12}) = \frac{1}{2}$ ，求cosA的值．

查看试题解析
21. 已知 $\vec{a}$ =（ $\sqrt{3}$ sinx，m+cosx）， $\vec{b}$ =（cosx，﹣m+cosx），且f（x）= $\vec{a} \cdot \vec{b}$

(1)、求函数f（x）的解析式；

(2)、当x∈ $[- \frac{π}{6} ， \frac{π}{3}]$ 时，f（x）的最小值是﹣4，求此时函数f（x）的最大值，并求出相应的x的值．

查看试题解析
22. 已知函数f（x）=2cosxsin（x﹣ $\frac{π}{6}$ ）+ $\frac{1}{2}$ ．

(1)、求函数f（x）的对称轴方程；

(2)、若方程sin2x+2|f（x+ $\frac{π}{12}$ ）|﹣m+1=0在x∈ $[- \frac{π}{3} ， \frac{π}{2}]$ 上有三个实数解，求实数m的取值范围．

查看试题解析