2016-2017学年湖北省孝感市七校联考高一下学期期中数学试卷（理科）

试卷更新日期：2017-06-22 类型：期中考试

进入出卷网下载

一、选择题

1. 已知集合A={x|﹣3＜x＜3}，B={x|y=lg（x+1）}，则集合A∩B为（）

A、[0，3） B、[﹣1，3） C、（﹣1，3） D、（﹣3，﹣1]

查看试题解析
2. 在等差数列{a_n}中，a₇a₁₁=6，a₄+a₁₄=5，则该数列公差d等于（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ 或 $- \frac{1}{2}$ C、﹣ $\frac{1}{4}$ D、 $\frac{1}{4}$ 或﹣ $\frac{1}{4}$

查看试题解析
3. △ABC的内角A，B，C的对边分别为a，b，c．若c=2，b= $\sqrt{7}$ ，B=120°，则a等于（）

A、 $\sqrt{6}$ B、1 C、 $\sqrt{3}$ D、3

查看试题解析
4. 设S_n为等比数列{a_n}的前n项和，且8a₂+a₅=0，则S₃：S₂的值为（）

A、﹣3 B、5 C、﹣8 D、﹣11

查看试题解析
5. 已知向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $60^{\circ} ， | \vec{a} | = 2 ， | \vec{b} | = 5$ ，则| $2 \vec{a} - \vec{b}$ |的值为（）

A、21 B、 $\sqrt{21}$ C、 $\sqrt{23}$ D、 $\sqrt{35}$

查看试题解析
6. 设等差数列{a_n}的前n项和为S_n ，若a₁=﹣11，a₄+a₆=﹣6，则a₃等于（）

A、16 B、37 C、﹣7 D、9

查看试题解析
7. △ABC的内角A，B，C所对的边分别为a，b，c．且a：b：c=3：5：7试判断该三角形的形状（）

A、钝角三角形 B、锐角三角形 C、直角三角形 D、等边三角形

查看试题解析
8. 已知平面向量 $\vec{a} ， \vec{b}$ 满足| $\vec{a}$ |=3，| $\vec{b}$ |=2， $\vec{a}$ ， $\vec{b}$ 的夹角为60°，若 $(\vec{a} - m \vec{b}) ⊥ \vec{a}$ ，则实数m的值为（）

A、1 B、 $\frac{3}{2}$ C、2 D、3

查看试题解析
9. 在△ABC中，A=60°，b=1，这个三角形的面积为 $\sqrt{3}$ ，则sin C的值为（）

A、 $\frac{\sqrt{3}}{8}$ B、 $\frac{\sqrt{15}}{8}$ C、 $\frac{2 \sqrt{39}}{13}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
10. 如图，正方形ABCD中，E为DC的中点，若 $\vec{A E}$ =λ $\vec{A B}$ +μ $\vec{A C}$ ，则λ+μ的值为（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、1 D、﹣1

查看试题解析
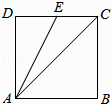11. 已知数列{a_n}中，a₁=1，a_n₊₁=2a_n+1（n∈N^*），S_n为其前n项和，则S₅的值为（）

A、57 B、61 C、62 D、63

查看试题解析
12. 已知f（x）是定义在R上的偶函数，且在（﹣∞，0]上是增函数，设 $a = f (\log_{4} 7) ， b = f (\log_{\frac{1}{2}} 3)$ ，c=f（0.2^0.6），则a，b，c的大小关系是（）

A、c＜b＜a B、b＜c＜a C、b＜a＜c D、a＜b＜c

查看试题解析

二、填空题

13. 函数 $f (x) = \log_{\frac{1}{2}} (x^{2} - 2 x - 3)$ 的单调递增区间是．

查看试题解析
14. 在我国古代著名的数学专著《九章算术》里有﹣段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里：驽马初日行九十七里，日减半里，良马先至齐，复还迎驽马，二马相逢，问：需日相逢．

查看试题解析
15. 已知在△ABC中，∠A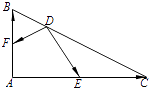= $\frac{π}{2}$ ，AB=2，AC=4， $\vec{A F}$ = $\frac{1}{2} \vec{A B}$ ， $\vec{C E}$ = $\frac{1}{2} \vec{C A}$ ， $\vec{B D}$ = $\frac{1}{4} \vec{B C}$ ，则 $\vec{D E}$ • $\vec{D F}$ 的值为．

查看试题解析
16. 已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x²+2x，若f（2﹣a²）＞f（a），则实数a的取值范围是．

查看试题解析

三、解答题

17. 已知关于x的不等式（m﹣1）x²+（m﹣1）x+2＞0

(1)、若m=0，求该不等式的解集

(2)、若该不等式的解集是R，求m的取值范围．

查看试题解析
18. 已知向量 $a = (3 ， 1)$ ， $b = (- 2 ， 4)$ ，向量 $a$ 与 $\vec{b}$ 夹角为θ；

(1)、求cosθ；

(2)、求 $a$ 在 $b$ 方向上的投影．

查看试题解析
19. 轮船A和轮船B在上午8时同时离开海港C，两船航行方向之间的夹角为120°，轮船A与轮船B的航行速度分别为25海里/小时和15海里/小时，则上午12时两船之间的距离是多少？

查看试题解析
20. 已知公差不为0的等差数列{a_n}中，a₁=2，且a₂+1，a₄+1，a₈+1成等比数列．

(1)、求数列{a_n}通项公式；

(2)、设数列{b_n}满足b_n= $\frac{3}{a_{n}}$ ，求适合方程b₁b₂+b₂b₃+…+b_nb_n₊₁= $\frac{45}{32}$ 的正整数n的值．

查看试题解析
21. 在△ABC中，角A，B，C所对的边分别为a，b，c，且a²+c²=b²﹣ac．

(1)、求B的大小；

(2)、设∠BAC的平分线AD交BC于D，AD=2 $\sqrt{3}$ ，BD=1，求cosC的值．

查看试题解析
22. 在单调递增数列{a_n}中，a₁=2，a₂=4，且a_2n_﹣₁ ， a_2n ， a_2n₊₁成等差数列，a_2n ， a_2n₊₁ ， a_2n₊₂成等比数列，n=1，2，3，…．
（Ⅰ）（ⅰ）求证：数列 ${\sqrt{a_{2 n}}}$ 为等差数列；
（ⅱ）求数列{a_n}的通项公式．
（Ⅱ）设数列 ${\frac{1}{a_{n}}}$ 的前n项和为S_n ，证明：S_n＞ $\frac{4 n}{3 (n + 3)}$ ，n∈N^* ．

查看试题解析