2016-2017学年湖北省鄂东南省级示范高中联考高一下学期期中数学试卷（理科）

试卷更新日期：2017-06-22 类型：期中考试

进入出卷网下载

一、选择题：

1. sin300°+cos390°+tan（﹣135°）=（）

A、 $\sqrt{3}$ ﹣1 B、1 C、 $\sqrt{3}$ D、 $\sqrt{3}$ +1

查看试题解析
2. 已知a= ${(\frac{1}{e})}^{x}$ ，b=x² ， c=lnx，其中e为自然对数的底数，则当x=e时，a，b，c的大小关系为（）

A、a＜b＜c B、a＜c＜b C、c＜b＜a D、c＜a＜b

查看试题解析
3. 已知等差数列{a_n}中，a₁+a₄+a₇= $\frac{5}{4} π$ ，那么cos（a₃+a₅）=（）

A、 $\frac{\sqrt{3}}{2}$ B、﹣ $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、﹣ $\frac{\sqrt{2}}{2}$

查看试题解析
4. 已知tan（α+β）= $\frac{2}{5}$ ，tan（ $β + \frac{π}{4}$ ）= $\frac{1}{4}$ ，则tan（ $α - \frac{π}{4}$ ）的值为（）

A、 $\frac{1}{6}$ B、 $\frac{22}{13}$ C、 $\frac{3}{22}$ D、 $\frac{13}{18}$

查看试题解析
5. 若函数y=f（x）的图象上每一点的纵坐标保持不变，横坐标伸长到原来的2倍，再将整个图象沿x轴向右平移 $\frac{π}{2}$ 个单位，沿y轴向下平移1个单位，得到函数y= $\frac{1}{2}$ sinx的图象，则y=f（x）的解析式为（）

A、y= $\frac{1}{2}$ sin（2x+ $\frac{π}{2}$ ）+1 B、y= $\frac{1}{2}$ sin（2x﹣ $\frac{π}{2}$ ）+1 C、y= $\frac{1}{2}$ sin（ $\frac{1}{2}$ x+ $\frac{π}{4}$ ）+1 D、y= $\frac{1}{2}$ sin（ $\frac{1}{2}$ x﹣ $\frac{π}{4}$ ）+1

查看试题解析
6. 函数f（x）=a^x+b﹣1（其中0＜a＜1且0＜b＜1）的图象一定不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 设函数f（x）=sin（2x+ $\frac{π}{6}$ ）+ $\sqrt{3}$ cos（2x+ $\frac{π}{6}$ ），则（）

A、y=f（x）在（0， $\frac{π}{2}$ ）单调递增，其图象关于直线x= $\frac{π}{4}$ 对称 B、y=f（x）在（0， $\frac{π}{2}$ ）单调递增，其图象关于直线x= $\frac{π}{2}$ 对称 C、y=f（x）在（0， $\frac{π}{2}$ ）单调递减，其图象关于直线x= $\frac{π}{4}$ 对称 D、y=f（x）在（0， $\frac{π}{2}$ ）单调递减，其图象关于直线x= $\frac{π}{2}$ 对称

查看试题解析
8. 设θ是第四象限角，则点P（sin（sinθ），cos（sinθ））在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 已知非零向量 $\vec{A B}$ 与 $\vec{A C}$ 满足（ $\frac{\vec{A B}}{\vec{| A B |}}$ + $\frac{\vec{A C}}{\vec{| A C |}}$ ）• $\vec{B C}$ =0，且 $\frac{\vec{A B}}{\vec{| A B |}}$ • $\frac{\vec{A C}}{\vec{| A C |}}$ =﹣ $\frac{1}{2}$ ，则△ABC为（）

A、等腰非等边三角形 B、等边三角形 C、三边均不相等的三角形 D、直角三角形

查看试题解析
10. 已知f（x）是奇函数，且对于任意x∈R满足f（2﹣x）=f（x），当0＜x≤1时，f（x）=lnx+2，则函数y=f（x）在（﹣2，4]上的零点个数是（）

A、7 B、8 C、9 D、10

查看试题解析
11. 已知a，b，c分别为△ABC的内角A，B，C所对的边，且3a²+3b²﹣c²=4ab，则△ABC（）

A、可能为锐角三角形 B、一定不是锐角三角形 C、一定为钝角三角形 D、不可能为钝角三角形

查看试题解析
12. 函数f（x）= $\frac{2 \sin x \cdot c o s x}{1 + \sin x + c o s x}$ ，x∈（0， $\frac{π}{2}$ ]的最大值M，最小值为N，则M﹣N=（）

A、 $\frac{\sqrt{2} - 1}{2}$ B、 $\sqrt{2}$ ﹣1 C、2 $\sqrt{2}$ D、 $\sqrt{2}$ +1

查看试题解析

二、填空题：

13. 已知 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 为单位向量且夹角为 $\frac{π}{3}$ ，设 $\vec{a}$ = $\vec{e_{1}}$ + $\vec{e_{2}}$ ， $\vec{b}$ = $\vec{e_{2}}$ ， $\vec{a}$ 在 $\vec{b}$ 方向上的投影为．

查看试题解析
14. 已知数列{a_n}满足a₁=1，a₂=0，a_n₊₂=a_n₊₁﹣a_n（n≥1），则a₂₀₁₇= ．

查看试题解析
15. 函数f（x）= ${\begin{matrix} {ax}^{2} - 6 x + a^{2} + 1 (x < 1) \\ x^{5 - 2 a} (x \geq 1) \end{matrix}$ 是R上的单调递减函数，则实数a的取值范围是．

查看试题解析
16. 在正项等差数列{a_n}中a₁和a₄是方程x²﹣10x+16=0的两个根，若数列{log₂a_n}的前5项和为S₅且S₅∈[n，n+1]，n∈Z，则n= ．

查看试题解析

三、解答题

17. 已知向量 $\vec{a}$ =（4，5cosα）， $\vec{b}$ =（3，﹣4tanα），α∈（0， $\frac{π}{2}$ ）， $\vec{a}$ ⊥ $\vec{b}$ ．

(1)、求| $\vec{a}$ ﹣ $\vec{b}$ |；

(2)、求cos（ $\frac{3 π}{2}$ +α）﹣sin（α﹣π）．

查看试题解析
18. 已知函数f（x）=cosωx•sin（ωx﹣ $\frac{π}{3}$ ）+ $\sqrt{3}$ cos²ωx﹣ $\frac{\sqrt{3}}{4}$ （ω＞0，x∈R），且函数y=f（x）图象的一个对称中心到它对称轴的最近距离为 $\frac{π}{4}$ ．

(1)、求ω的值及f（x）的对称轴方程；

(2)、在△ABC中，角A，B，C的对边分别为a，b，c，若f（A）=0，sinB= $\frac{4}{5}$ ，a= $\sqrt{3}$ ，求b的值．

查看试题解析
19. 已知函数y=log₂（ax²﹣2x+2）的定义域为Q．

(1)、若a＞0且[2，3]∩Q=∅，求实数a的取值范围；

(2)、若[2，3]⊆Q，求实数a的取值范围．

查看试题解析
20. 在等差数列{a_n}中，a₁₅+a₁₆+a₁₇=﹣45，a₉=﹣36，S_n为其前n项和．

(1)、求S_n的最小值，并求出相应的n值；

(2)、求T_n=|a₁|+|a₂|+…+|a_n|．

查看试题解析
21.
如图，为迎接校庆，我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”，规划在△ABD的内接正方形BEFG内种花，其余地方种草，若AB=a，∠DAB=θ，种草的面积为S₁ ，种花的面积为S₂ ，比值 $\frac{S_{1}}{S_{2}}$ 称为“规划和谐度”．

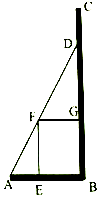(1)、试用a，θ表示S₁ ， S₂；

(2)、若a为定值，BC足够长，当θ为何值时，“规划和谐度”有最小值，最小值是多少？

查看试题解析
22. 已知定义域为[0，e]的函数f（x）同时满足：
①对于任意的x∈[0，e]，总有f（x）≥0；
②f（e）=e；
③若x₁≥0，x₂≥0，x₁+x₂≤e，则恒有f（x₁+x₂）≥f（x₁）+f（x₂）．

(1)、求f（0）的值；

(2)、证明：不等式f（x）≤e对任意x∈[0，e]恒成立；

(3)、若对于任意x∈[0，e]，总有4f²（x）﹣4（2e﹣a）f（x）+4e²﹣4ea+1≥0，求实数a的取值范围．

查看试题解析