分式与分式方程的复习
试卷更新日期:2017-06-21 类型:单元试卷
一、单选题
-
1. 在式子 , , , 中,分式的个数为( )A、1个 B、2个 C、3个 D、4个2. 使分式 有意义,x应满足的条件是( )A、x≠1 B、x≠2 C、x≠1或x≠2 D、x≠1且x≠23.
若方程 =0有增根,则增根可能是( )
A、0或2 B、0 C、2 D、14. 下列运算中正确的是( )A、 B、 C、 D、5. 计算 的值等于( )A、﹣9a B、9a C、﹣36a D、36a6. 化简 ,其结果是( )A、 B、 C、 D、7. 若关于x的分是方程+=2有增根,则m的值是( )A、m=﹣1 B、m=0 C、m=3 D、m=0或m=3二、填空题
-
8. 当x时,式子 有意义;当x时,分式 的值为零.9. 已知分式 ,当x=2时,分式的值为0;当x=﹣2时,分式无意义,则mn= .10. 已知x+y=5,xy=2,则 + = .11. 若关于x的分式方程 有增根,则实数a= .12.
若分式 的值等于5,则a的值是 。
13. 计算 的结果为 .14.化简 =.
三、计算题
-
15. 计算: .16. 计算:
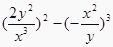
 .
.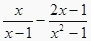 =1.
=1.