2016-2017学年湖北省部分重点中学高一下学期期中数学试卷（理科）

试卷更新日期：2017-06-21 类型：期中考试

进入出卷网下载

一、选择题

1. 等差数列{a_n}中，a₇+a₉=16，a₄=2，则a₁₂=（）

A、10 B、14 C、15 D、30

查看试题解析
2. 如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为（　　）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、由增加的长度决定

查看试题解析
3. 数列{a_n}中，已知对任意n∈N^* ， a₁+a₂+a₃+…+a_n=3ⁿ﹣1，则a₁²+a₂²+a₃²+…+a_n²等于（）

A、（3ⁿ﹣1）² B、 $\frac{1}{2} (9^{n} - 1)$ C、9ⁿ﹣1 D、 $\frac{1}{4} (3^{n} - 1)$

查看试题解析
4. 如图，在平行四边形ABCD中，M、N分别为AB、AD上的点，且 $\frac{1}{2}$ = $\frac{4}{5}$ $\vec{A B}$ ， $\vec{A N}$ = $\frac{2}{3}$ $\vec{A D}$ ，连接AC、MN交于P点，若 $\vec{A P}$ =λ $\vec{A C}$ ，则λ的值为（）

A、 $\frac{3}{5}$ B、 $\frac{3}{7}$ C、 $\frac{4}{11}$ D、 $\frac{4}{13}$

查看试题解析
5. 古代数字著作《九章算术》有如下问题：“今有女子善织，日自倍，五日五尺，问日织几何？”意思是：“一女子善于织布，每天织的布都是前一天的2倍，已知她5天共织布5尺，问这女子每天分别织布多少？”根据上题的已知条件，若要使织布的总尺数不少于50尺，该女子所需的天数至少为（）

A、7 B、8 C、9 D、10

查看试题解析
6. 公差不为0的等差数列{a_n}的部分项 $a k_{1}$ ， $a k_{2}$ ， $a k_{s}$ ，…构成等比数列{ $a k_{n}$ }，且k₁=1，k₂=2，k₃=6，则k₅为（）

A、86 B、88 C、90 D、92

查看试题解析
7. 如图，在等腰直角△ABO中，设 $\vec{O A}$ = $\vec{a}$ ， $\vec{O B}$ = $\vec{b}$ ，| $\vec{O A}$ |=| $\vec{O B}$ |=1，C为AB上靠近A点的三等分点，过C作AB的垂线l，设P为垂线上任一点， $\vec{O P}$ = $\vec{p}$ ，则 $\vec{p}$ •（ $\vec{b}$ ﹣ $\vec{a}$ ）=（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、﹣ $\frac{3}{2}$ D、 $\frac{3}{2}$

查看试题解析
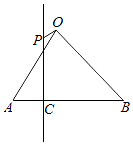8. 已知A，B是单位圆上的两点，O为圆心，且∠AOB=90°，MN是圆O的一条直径，点C在圆内，且满足 $\vec{O C}$ =λ $\vec{O A}$ +（1﹣λ） $\vec{O B}$ （λ∈R），则 $\vec{C M}$ • $\vec{C N}$ 的最小值为（）

A、﹣ $\frac{1}{2}$ B、﹣ $\frac{1}{4}$ C、﹣ $\frac{3}{4}$ D、﹣1

查看试题解析
9. 设等差数列{a_n}的前n项和为S_n且满足S₁₅＞0，S₁₆＜0则 $\frac{S_{1}}{a_{1}} ， \frac{S_{2}}{a_{2}} ， \frac{S_{3}}{a_{3}} ， \dots ， \frac{S_{15}}{a_{15}}$ 中最大的项为（）

A、 $\frac{S_{6}}{a_{6}}$ B、 $\frac{S_{7}}{a_{7}}$ C、 $\frac{S_{8}}{a_{8}}$ D、 $\frac{S_{9}}{a_{9}}$

查看试题解析
10. 已知△AOB中，∠AOB=120°，| $\vec{O A}$ |=3，| $\vec{O B}$ |=2，过O作OD垂直AB于点D，点E为线段OD的中点，则 $\vec{O E}$ • $\vec{E A}$ 的值为（）

A、 $\frac{5}{19}$ B、 $\frac{27}{76}$ C、 $\frac{3}{76}$ D、 $\frac{3}{19}$

查看试题解析
11. 如图，已知点D为△ABC的边BC上一点， $\vec{B D}$ =3 $\vec{D C}$ ，E_n（n∈N₊）为边AC上的点，满足 $\vec{E_{n} A}$ = $\frac{1}{4}$ a_n₊₁ ， $\vec{E_{n} B}$ =（4a_n+3） $\vec{E_{n} D}$ ，其中实数列{a_n}中a_n＞0，a₁=1，则{a_n}的通项公式为（）

A、3•2ⁿ^﹣¹﹣2 B、2ⁿ﹣1 C、4ⁿ﹣2 D、2•4ⁿ^﹣¹﹣1

查看试题解析
12. 已知数列{a_n}满足：a_n₊₁＞2a_n﹣a_n_﹣₁（n＞1．n∈N^*），给出下述命题：
①若数列{a_n}满足：a₂＞a₁ ，则a_n＞a_n_﹣₁（n＞1，n∈N^*）成立；
②存在常数c，使得a_n＞c（n∈N^*）成立；
③若p+q＞m+n（其中p，q，m，n∈N^*），则a_p+a_q＞a_m+a_n；
④存在常数d，使得a_n＞a₁+（n﹣1）d（n∈N^*）都成立
上述命题正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 设数列{a_n}的前n项和为S_n ，且a₁=﹣1，a_n₊₁=S_n•S_n₊₁ ，则数列{a_n}的通项公式a_n= ．

查看试题解析
14. 如图，在△ABC中，已知∠BAC= $\frac{π}{3}$ ，| $\vec{A B}$ |=2，| $\vec{A C}$ |=3，点D为边BC上一点，满足 $\vec{A C}$ +2 $\vec{A B}$ =3 $\vec{A D}$ ，点E是AD上一点，满足 $\vec{A E}$ =2 $\vec{E D}$ ，则| $\vec{B E}$ |= ．

查看试题解析
15. 如图所示，在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD，为了测量该山坡相对于水平地面的坡角θ，在山坡的A处测得∠DAC=15°，沿山坡前进50m到达B处，又测得∠DBC=45°，根据以上数据可得cosθ= ．

查看试题解析
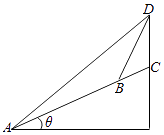16. 点O是平面上一定点，A、B、C是平面上△ABC的三个顶点，∠B、∠C分别是边AC、AB的对角，以下命题正确的是（把你认为正确的序号全部写上）．
①动点P满足 $\vec{O P}$ = $\vec{O A}$ + $\vec{P B}$ + $\vec{P C}$ ，则△ABC的重心一定在满足条件的P点集合中；
②动点P满足 $\vec{O P}$ = $\vec{O A}$ +λ（ $\frac{\vec{A B}}{| \vec{A B} |}$ + $\frac{\vec{A C}}{| \vec{A C} |}$ ）（λ＞0），则△ABC的内心一定在满足条件的P点集合中；
③动点P满足 $\vec{O P}$ = $\vec{O A}$ +λ（ $\frac{\vec{A B}}{| \vec{A B} | \sin B}$ + $\frac{\vec{A C}}{| \vec{A C} | \sin C}$ ）（λ＞0），则△ABC的重心一定在满足条件的P点集合中；
④动点P满足 $\vec{O P}$ = $\vec{O A}$ +λ（ $\frac{\vec{A B}}{| \vec{A B} | \cos B}$ + $\frac{\vec{A C}}{| \vec{A C} | \cos C}$ ）（λ＞0），则△ABC的垂心一定在满足条件的P点集合中；
⑤动点P满足 $\vec{O P}$ = $\frac{\vec{O B} + \vec{O C}}{2}$ +λ（ $\frac{\vec{A B}}{| \vec{A B} | \cos B}$ + $\frac{\vec{A C}}{| \vec{A C} | \cos C}$ ）（λ＞0），则△ABC的外心一定在满足条件的P点集合中．

查看试题解析

三、解答题

17. 在△ABC中，角A、B、C所对的边分别为a、b、c，设向量 $\vec{π}$ =（a，c）， $\vec{n}$ =（cosC，cosA）．

(1)、若 $\vec{π}$ ∥ $\vec{n}$ ，a= $\sqrt{3}$ c，求角A；

(2)、若 $\vec{π}$ • $\vec{n}$ =3bsinB，cosA= $\frac{3}{5}$ ，求cosC的值．

查看试题解析
18. 设数列{a_n}的前n项和为S_n ，已知a₁=1，a_n₊₁= $\frac{2 n + 3}{n}$ S_n（n∈N^*）．

(1)、证明：数列{ $\frac{S_{n}}{n}$ }是等比数列；

(2)、求数列{S_n}的前n项和T_n ．

查看试题解析
19. 如图，已知O为△ABC的外心，角A、B、C的对边分别为a、b、c．

(1)、若5 $\vec{O A}$ +4 $\vec{O B}$ +3 $\vec{O C}$ = $\vec{0}$ ，求cos∠BOC的值；

(2)、若 $\vec{C O}$ • $\vec{A B}$ = $\vec{B O}$ • $\vec{C A}$ ，求 $\frac{b^{2} + c^{2}}{a^{2}}$ 的值．

查看试题解析
20. 如图，D、E分别是△ABC的三等分点，设 $\vec{A D}$ = $\vec{π}$ ， $\vec{A E}$ = $\vec{n}$ ，∠BAC= $\frac{π}{3}$ ．

(1)、用 $\vec{π}$ ， $\vec{n}$ 分别表示 $\vec{A B}$ ， $\vec{A C}$ ；

(2)、若 $\vec{A D}$ • $\vec{A E}$ =15，| $\vec{B C}$ |=3 $\sqrt{3}$ ，求△ABC的面积．

查看试题解析
21. △ABC的三个内角A、B、C所对的边分别为a、b、c，1+ $\frac{\tan A}{tanB}$ = $\frac{2 c}{b}$ ．

(1)、求A的大小；

(2)、若△ABC为锐角三角形，求函数y=2sin²B﹣2cosBcosC的取值范围；

(3)、现在给出下列三个条件：①a=1；②2c﹣（ $\sqrt{3}$ +1）b=0；③B=45°，试从中再选择两个条件，以确定△ABC，求出所确定的△ABC的面积．

查看试题解析
22. 已知数列{a_n}为等差数列，a₁=2，{a_n}的前n项和为S_n ，数列{b_n}为等比数列，且a₁b₁+a₂b₂+a₃b₃+…+a_nb_n=（n﹣1）•2ⁿ⁺²+4对任意的n∈N*恒成立．

(1)、求数列{a_n}、{b_n}的通项公式；

(2)、是否存在非零整数λ，使不等式sin $\frac{a_{n} π}{4}$ ＜ $\frac{1}{λ (1 - \frac{1}{a_{1}}) (1 - \frac{1}{a_{2}}) \dots (1 - \frac{1}{a_{n}}) \sqrt{a_{n} + 1}}$ 对一切n∈N^*都成立？若存在，求出λ的值；若不存在，说明理由．

(3)、各项均为正整数的无穷等差数列{c_n}，满足c₃₉=a₁₀₀₇ ，且存在正整数k，使c₁ ， c₃₉ ， c_k成等比数列，若数列{c_n}的公差为d，求d的所有可能取值之和．

查看试题解析