2016-2017学年湖北省“荆、荆、襄、宜”四地七校联盟高一下学期期中数学试卷

试卷更新日期：2017-06-21 类型：期中考试

进入出卷网下载

一、选择题

1. 设集合M={x|x²=x}，N={x|lgx≤0}，则M∪N=（　　）

A、[0，1] B、（0，1] C、[0，1） D、（﹣∞，1]

查看试题解析
2. 下列函数中，在区间（﹣∞，0）上是增函数的是（）

A、 $y = 1 - \frac{1}{x - 1}$ B、y=|x﹣1| C、y=x²﹣4x+8 D、 $y = \sqrt{1 - x}$

查看试题解析
3. 等差数列的前4项之和为30，前8项之和为100，则它的前12项之和为（）

A、130 B、170 C、210 D、260

查看试题解析
4. 已知点A（1，1），B（4，2）和向量 $\vec{a}$ =（2，λ），若 $\vec{a}$ ∥ $\vec{A B}$ ，则实数λ的值为（）

A、﹣ $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、﹣ $\frac{3}{2}$

查看试题解析
5. 在平面直角坐标系中，若角α的顶点与原点重合，始边与x轴的非负半轴重合，终边过点P（﹣ $\sqrt{3}$ ，﹣1），则sin（ $\frac{π}{2}$ ﹣α）=（）

A、 $\frac{\sqrt{3}}{2}$ B、 $- \frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
6. 若等比数列{a_n}的各项均为正数，且a₈a₁₃+a₉a₁₂=2⁶ ，则log₂a₁+log₂a₂+…+log₂a₂₀=（）

A、120 B、100 C、50 D、60

查看试题解析
7. 如图所示，为测一树的高度，在地面上选取A、B两点，从A、B两点分别测得树尖的仰角为30°、45°，且A、B两点之间的距离为60m，则树的高度为（）

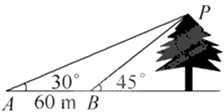A、（30+30 $\sqrt{3}$ ） m B、（30+15 $\sqrt{3}$ ） m C、（15+30 $\sqrt{3}$ ） m D、（15+15 $\sqrt{3}$ ） m

查看试题解析
8. 函数f（x）=Asin（ωx+φ）（其中 $A > 0 ， | ϕ | < \frac{π}{2}$ ）的图象如图所示，为了得到g（x）=sin2x的图象，则只需将f（x）的图象（）

A、向右平移 $\frac{π}{6}$ 个长度单位 B、向右平移 $\frac{π}{12}$ 个长度单位 C、向左平移 $\frac{π}{6}$ 个长度单位 D、向左平移 $\frac{π}{12}$ 个长度单位

查看试题解析
9. 已知函数y=f（x）是定义在R上的偶函数，且在（﹣∞，0]上是增函数，若不等式f（a）≥f（x）对任意x∈[1，2]恒成立，则实数a的取值范围是（）

A、（﹣∞，1] B、[﹣1，1] C、（﹣∞，2] D、[﹣2，2]

查看试题解析
10. 在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．若sinC+sin（B﹣A）=sin2A，则△ABC的形状为（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形

查看试题解析
11. 已知函数y=sin（πx+φ）﹣2cos（πx+φ）（0＜φ＜π）的图象关于点（1，0）对称，则tanφ=（）

A、﹣ $\frac{1}{2}$ B、﹣2 C、 $\frac{1}{2}$ D、2

查看试题解析
12. 已知等差数列{a_n}满足 $\frac{\sin^{2} a_{6} \cos^{2} a_{9} - \sin^{2} a_{9} \cos^{2} a_{6}}{\sin (a_{7} + a_{8})}$ =1，公差d∈（﹣1，0），当且仅当n=9时，数列{a_n}的前n项和S_n取得最大值，则该数列首项a₁的取值范围是（）

A、（ $\frac{4 π}{3}$ ， $\frac{3 π}{2}$ ） B、[ $\frac{4 π}{3}$ ， $\frac{3 π}{2}$ ] C、（ $\frac{7 π}{6}$ ， $\frac{4 π}{3}$ ） D、[ $\frac{7 π}{6}$ ， $\frac{4 π}{3}$ ]

查看试题解析

二、填空题

13. 已知函数f（x）=x²﹣2（a﹣1）x+2在区间（﹣∞，5]上为减函数，则实数a的取值范围为．

查看试题解析
14. 已知sinα+cosα= $\frac{2}{3}$ ，则cos2α= ．

查看试题解析
15. 在直角三角形ABC中，∠ACB=90°，AC=BC=2，点P是斜边AB上的一个三等分点，则 $\vec{C P} • \vec{C B} + \vec{C P} • \vec{C A}$ = ．

查看试题解析
16. 在△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinb，且 $B > \frac{π}{2}$ ，则sinA+sinC的最大值是．

查看试题解析

三、解答题

17. 已知等差数列{a_n}的前n项和S_n ，且a₃=7，S₁₁=143，
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n=2 $^{a_{n}}$ +2n，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 已知向量 $\vec{α}$ =（{cosx，﹣ $\sqrt{3}$ cosx）， $\vec{b}$ =（cosx，sinx），函数f（x）= $\vec{α}$ • $\vec{b}$ +1．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若f（θ）= $\frac{5}{6}$ ， $θ \in (\frac{π}{3} ， \frac{2 π}{3}) ，求 \sin 2 θ$ 的值．

查看试题解析
19. 某种新产品投放市场的100天中，前40天价格呈直线上升，而后60天其价格呈直线下降，现统计出其中4天的价格如下表：
时间
第4天
第32天
第60天
第90天
价格（千元）
23
30
22
7
（Ⅰ）写出价格f（x）关于时间x的函数关系式（x表示投放市场的第x天，x∈N^*）；
（Ⅱ）销售量g（x）与时间x的函数关系式为 $g (x) = \frac{1}{3} x + \frac{100}{9} (1 \leq x \leq 100 ， x \in N^{*})$ ，则该产品投放市场第几天的销售额最高？最高为多少千元？

查看试题解析
20. 已知数列{a_n}中， $a_{1} = 1 ， a_{n + 1} = \frac{a_{n}}{a_{n} + 2} (n \in N^{*})$
（Ⅰ）求证： ${\frac{1}{a_{n}} + 1}$ 是等比数列，并求{a_n}的通项公式a_n；
（Ⅱ）数列{b_n}满足 $b_{n} = (2^{n} - 1) \cdot \frac{n}{2^{n - 1}} \cdot a_{n}$ ，数列{b_n}的前n项和为T_n ，若不等式 ${(- 1)}^{n} λ < T_{n} + \frac{n}{2^{n - 1}}$ 对一切n∈N^*恒成立，求λ的取值范围．

查看试题解析
21. 已知函数f（x）=log_a（x+1），g（x）=2log_a（2x+t）（t∈R），a＞0，且a≠1．
（Ⅰ）若3是关于x的方程f（x）﹣g（x）=0的一个解，求t的值；
（Ⅱ）当0＜a＜1且t=1时，解不等式f（x）≤g（x）；
（Ⅲ）若函数F（x）=a^f^（^x^）+tx²﹣2t+1在区间（﹣1，3]上有零点，求t的取值范围．

查看试题解析
22. 在△ABC中，已知B=45°，D是BC上一点，AD=5，AC=7，DC=3，求AB的长．

查看试题解析

时间	第4天	第32天	第60天	第90天
价格（千元）	23	30	22	7