2017年江苏省苏州市中考数学试卷
试卷更新日期:2017-06-21 类型:中考真卷
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 的结果是( )
A、 B、 C、 D、2. 有一组数据: , , , , ,这组数据的平均数为( )A、 B、 C、 D、3. 小亮用天平称得一个罐头的质量为 ,用四舍五入法将 精确到 的近似值为( )A、 B、 C、 D、4. 关于 的一元二次方程 有两个相等的实数根,则 的值为( )
A、 B、 C、 D、5. 为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,并设置了“赞成、反对、无所谓”三种意见.现从学校所有 名学生中随机征求了 名学生的意见,其中持“反对”和“无所谓”意见的共有 名学生,估计全校持“赞成”意见的学生人数约为( )
A、 B、 C、 D、6. 若点 在一次函数 的图像上,且 ,则 的取值范围为( )
A、 B、 C、 D、7. 如图,在正五边形 中,连接 ,则 的度数为( )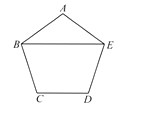 A、 B、 C、 D、8. 若二次函数 的图像经过点 ,则关于 的方程 的实数根为( )A、 , B、 , C、 , D、 ,9. 如图,在 中, , .以 为直径的 交 于点 , 是 上一点,且 ,连接 ,过点 作 ,交 的延长线于点 ,则 的度数为( )
A、 B、 C、 D、8. 若二次函数 的图像经过点 ,则关于 的方程 的实数根为( )A、 , B、 , C、 , D、 ,9. 如图,在 中, , .以 为直径的 交 于点 , 是 上一点,且 ,连接 ,过点 作 ,交 的延长线于点 ,则 的度数为( )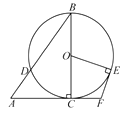 A、 B、 C、 D、10. 如图,在菱形 中, , , 是 的中点.过点 作 ,垂足为 .将 沿点 到点 的方向平移,得到 .设 、 分别是 、 的中点,当点 与点 重合时,四边形 的面积为( )
A、 B、 C、 D、10. 如图,在菱形 中, , , 是 的中点.过点 作 ,垂足为 .将 沿点 到点 的方向平移,得到 .设 、 分别是 、 的中点,当点 与点 重合时,四边形 的面积为( )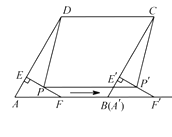 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,满分24分,将答案填在答题纸上)
-
11. 计算: .12. 如图,点 在 的平分线 上,点 在 上, , ,则 的度数为 .
 13. 某射击俱乐部将 名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图.由图可知, 名成员射击成绩的中位数是环.
13. 某射击俱乐部将 名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图.由图可知, 名成员射击成绩的中位数是环. 14. 因式分解: .15. 如图,在“ ”网格中,有 个涂成黑色的小方格.若再从余下的 个小方格中随机选取 个涂成黑色,则完成的图案为轴对称图案的概率是 .
14. 因式分解: .15. 如图,在“ ”网格中,有 个涂成黑色的小方格.若再从余下的 个小方格中随机选取 个涂成黑色,则完成的图案为轴对称图案的概率是 .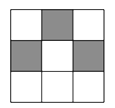 16. 如图, 是 的直径, 是弦, , .若用扇形 (图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 .
16. 如图, 是 的直径, 是弦, , .若用扇形 (图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 .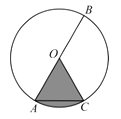 17. 如图,在一笔直的沿湖道路 上有 、 两个游船码头,观光岛屿 在码头 北偏东 的方向,在码头 北偏西 的方向, .游客小张准备从观光岛屿 乘船沿 回到码头 或沿 回到码头 ,设开往码头 、 的游船速度分别为 、 ,若回到 、 所用时间相等,则 (结果保留根号).
17. 如图,在一笔直的沿湖道路 上有 、 两个游船码头,观光岛屿 在码头 北偏东 的方向,在码头 北偏西 的方向, .游客小张准备从观光岛屿 乘船沿 回到码头 或沿 回到码头 ,设开往码头 、 的游船速度分别为 、 ,若回到 、 所用时间相等,则 (结果保留根号). 18. 如图,在矩形 中,将 绕点 按逆时针方向旋转一定角度后, 的对应边 交 边于点 .连接 、 ,若 , , ,则 (结果保留根号).
18. 如图,在矩形 中,将 绕点 按逆时针方向旋转一定角度后, 的对应边 交 边于点 .连接 、 ,若 , , ,则 (结果保留根号).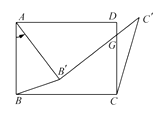
三、解答题 (本大题共10小题,共76分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算: .20. 解不等式组: .21. 先化简,再求值: ,其中 .22. 某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费 (元)是行李质量 ( )的一次函数.已知行李质量为 时需付行李费 元,行李质量为 时需付行李费 元.
(1)、当行李的质量 超过规定时,求 与 之间的函数表达式;(2)、求旅客最多可免费携带行李的质量.23. 初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.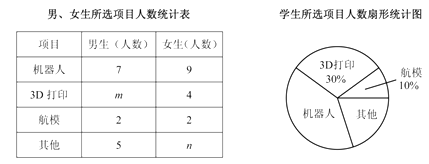
根据以上信息解决下列问题:
(1)、 , ;
(2)、扇形统计图中机器人项目所对应扇形的圆心角度数为 ;(3)、从选航模项目的 名学生中随机选取 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的 名学生中恰好有 名男生、 名女生的概率.24. 如图, , ,点 在 边上, , 和 相交于点 .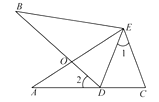 (1)、求证: ≌ ;
(1)、求证: ≌ ;
(2)、若 ,求 的度数.25. 如图,在 中, , 轴,垂足为 .反比例函数 ( )的图像经过点 ,交 于点 .已知 , .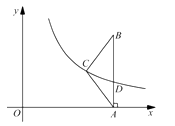 (1)、若 ,求 的值;(2)、连接 ,若 ,求 的长.26. 某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点 出发,在矩形 边上沿着 的方向匀速移动,到达点 时停止移动.已知机器人的速度为 个单位长度/ ,移动至拐角处调整方向需要 (即在 、 处拐弯时分别用时 ).设机器人所用时间为 时,其所在位置用点 表示, 到对角线 的距离(即垂线段 的长)为 个单位长度,其中 与 的函数图象如图②所示.
(1)、若 ,求 的值;(2)、连接 ,若 ,求 的长.26. 某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点 出发,在矩形 边上沿着 的方向匀速移动,到达点 时停止移动.已知机器人的速度为 个单位长度/ ,移动至拐角处调整方向需要 (即在 、 处拐弯时分别用时 ).设机器人所用时间为 时,其所在位置用点 表示, 到对角线 的距离(即垂线段 的长)为 个单位长度,其中 与 的函数图象如图②所示. (1)、求 、 的长;(2)、如图②,点 、 分别在线段 、 上,线段 平行于横轴, 、 的横坐标分别为 、 .设机器人用了 到达点 处,用了 到达点 处(见图①).若 ,求 、 的值.27. 如图,已知 内接于 , 是直径,点 在 上, ,过点 作 ,垂足为 ,连接 交 边于点 .
(1)、求 、 的长;(2)、如图②,点 、 分别在线段 、 上,线段 平行于横轴, 、 的横坐标分别为 、 .设机器人用了 到达点 处,用了 到达点 处(见图①).若 ,求 、 的值.27. 如图,已知 内接于 , 是直径,点 在 上, ,过点 作 ,垂足为 ,连接 交 边于点 .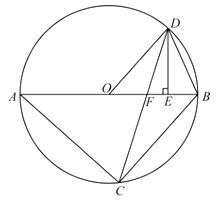 (1)、求证: ∽ ;(2)、求证: ;(3)、连接 ,设 的面积为 ,四边形 的面积为 ,若 ,求 的值.28. 如图,二次函数 的图像与 轴交于 、 两点,与 轴交于点 , .点 在函数图象上, 轴,且 ,直线 是抛物线的对称轴, 是抛物线的顶点.
(1)、求证: ∽ ;(2)、求证: ;(3)、连接 ,设 的面积为 ,四边形 的面积为 ,若 ,求 的值.28. 如图,二次函数 的图像与 轴交于 、 两点,与 轴交于点 , .点 在函数图象上, 轴,且 ,直线 是抛物线的对称轴, 是抛物线的顶点.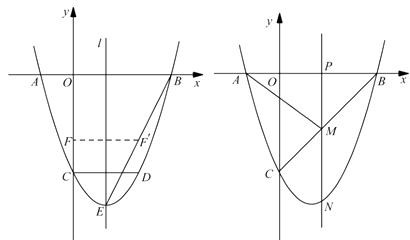
图 ① 图②
(1)、求 、 的值;(2)、如图①,连接 ,线段 上的点 关于直线 的对称点 恰好在线段 上,求点 的坐标;(3)、如图②,动点 在线段 上,过点 作 轴的垂线分别与 交于点 ,与抛物线交于点 .试问:抛物线上是否存在点 ,使得 与 的面积相等,且线段 的长度最小?如果存在,求出点 的坐标;如果不存在,说明理由.