2017年四川省自贡市中考数学试卷
试卷更新日期:2017-06-21 类型:中考真卷
一、一.选择题
-
1. 计算(﹣1)2017的结果是( )A、﹣1 B、1 C、﹣2017 D、20172. 下列成语描述的事件为随机事件的是( )A、水涨船高 B、守株待兔 C、水中捞月 D、缘木求鱼3. 380亿用科学记数法表示为( )A、38×109 B、0.38×1013 C、3.8×1011 D、3.8×10104. 不等式组 的解集表示在数轴上正确的是( )A、
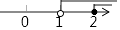 B、
B、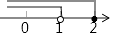 C、
C、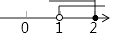 D、
D、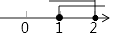 5. 如图,a∥b,点B在直线a上,且AB⊥BC,∠1=35°,那么∠2=( )
5. 如图,a∥b,点B在直线a上,且AB⊥BC,∠1=35°,那么∠2=( )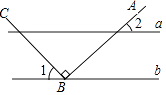 A、45° B、50° C、55° D、60°6. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
A、45° B、50° C、55° D、60°6. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、 B、
B、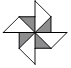 C、
C、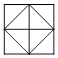 D、
D、 7. 对于一组统计数据3,3,6,5,3.下列说法错误的是( )A、众数是3 B、平均数是4 C、方差是1.6 D、中位数是68. 下面是几何体中,主视图是矩形的( )A、
7. 对于一组统计数据3,3,6,5,3.下列说法错误的是( )A、众数是3 B、平均数是4 C、方差是1.6 D、中位数是68. 下面是几何体中,主视图是矩形的( )A、 B、
B、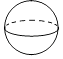 C、
C、 D、
D、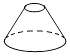 9. 下列四个命题中,其正确命题的个数是( )
9. 下列四个命题中,其正确命题的个数是( )①若a>b,则 > ;②垂直于弦的直径平分弦;③平行四边形的对角线互相平分;④反比例函数y= ,当k<0时,y随x的增大而增大.
A、1 B、2 C、3 D、410. AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C;连接BC,若∠P=40°,则∠B等于( )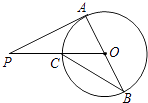 A、20° B、25° C、30° D、40°11.
A、20° B、25° C、30° D、40°11.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m的值为( )
 A、180 B、182 C、184 D、18612. 一次函数y1=k1x+b和反比例函数y2= (k1•k2≠0)的图象如图所示,若y1>y2 , 则x的取值范围是( )
A、180 B、182 C、184 D、18612. 一次函数y1=k1x+b和反比例函数y2= (k1•k2≠0)的图象如图所示,若y1>y2 , 则x的取值范围是( ) A、﹣2<x<0或x>1 B、﹣2<x<1 C、x<﹣2或x>1 D、x<﹣2或0<x<1
A、﹣2<x<0或x>1 B、﹣2<x<1 C、x<﹣2或x>1 D、x<﹣2或0<x<1二、填空题
-
13. 计算(﹣ )﹣1= .14. 在△ABC中,MN∥BC 分别交AB,AC于点M,N;若AM=1,MB=2,BC=3,则MN的长为 .
 15. 我国明代数学家程大位的名著《直接算法统宗》里有一道著名算题:
15. 我国明代数学家程大位的名著《直接算法统宗》里有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,正好分完;如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各几人?设大、小和尚各有x,y人,则可以列方程组 .
16. 圆锥的底面周长为6πcm,高为4cm,则该圆锥的全面积是;侧面展开扇形的圆心角是 .17. 如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD= ,则AD= .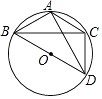 18.
18.如图,13个边长为1的小正方形,排列形式如图,把它们分割,使分割后能拼成一个大正方形.请在如图所示的网格中(网格的边长为1)中,用直尺作出这个大正方形.

三、解答题
-
19. 计算:4sin45°+|﹣2|﹣ +( )0 .20. 先化简,再求值:(a+ )÷ ,其中a=2.21. 如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.
求证:∠ABF=∠CBE.
 22.
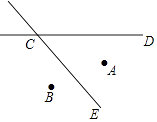
22.两个城镇A,B与一条公路CD,一条河流CE的位置如图所示,某人要修建一避暑山庄,要求该山庄到A,B的距离必须相等,到CD和CE的距离也必须相等,且在∠DCE的内部,请画出该山庄的位置P.(不要求写作法,保留作图痕迹.)
 23. 某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
23. 某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.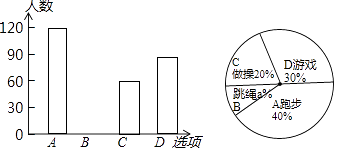
请结合统计图,回答下列问题:
(1)、本次调查学生共人,a= , 并将条形图补充完整;(2)、如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?(3)、学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.24. 【探究函数y=x+ 的图象与性质】(1)、函数y=x+ 的自变量x的取值范围是;(2)、下列四个函数图象中函数y=x+ 的图象大致是;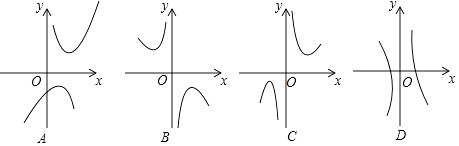 (3)、对于函数y=x+ ,求当x>0时,y的取值范围.
(3)、对于函数y=x+ ,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
解:∵x>0
∴y=x+ =( )2+( )2=( ﹣ )2+
∵( ﹣ )2≥0
∴y≥ .
(4)、若函数y= ,则y的取值范围 .25. 如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0, ). (1)、求∠BAO的度数;(2)、如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
(1)、求∠BAO的度数;(2)、如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.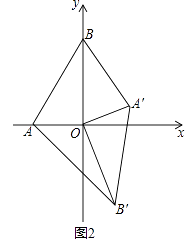 26. 抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.(1)、设AB=2,tan∠ABC=4,求该抛物线的解析式;(2)、在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;(3)、是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
26. 抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.(1)、设AB=2,tan∠ABC=4,求该抛物线的解析式;(2)、在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;(3)、是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.