2017年四川省成都市中考数学试卷（a卷）

试卷更新日期：2017-06-21 类型：中考真卷

进入出卷网下载

一、选择题

1. 《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数，若气温为零上10℃记作+10℃，则﹣3℃表示气温为（）

A、零上3℃ B、零下3℃ C、零上7℃ D、零下7℃

查看试题解析
2. 如图所示的几何体是由4个大小相同的小立方体组成，其俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 总投资647亿元的西域高铁预计2017年11月竣工，届时成都到西安只需3小时，上午游武侯区，晚上看大雁塔将成为现实，用科学记数法表示647亿元为（）

A、647×10⁸ B、6.47×10⁹ C、6.47×10¹⁰ D、6.47×10¹¹

查看试题解析
4. 二次根式 $\sqrt{x - 1}$ 中，x的取值范围是（）

A、x≥1 B、x＞1 C、x≤1 D、x＜1

查看试题解析
5. 下列图标中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列计算正确的是（）

A、a⁵+a⁵=a¹⁰ B、a⁷÷a=a⁶ C、a³•a²=a⁶ D、（﹣a³）²=﹣a⁶

查看试题解析
7. 学习全等三角形时，数学兴趣小组设计并组织了“生活中的全等”的比赛，全班同学的比赛结果统计如下表：
得分（分）
60
70
80
90
100
人数（人）
7
12
10
8
3
则得分的众数和中位数分别为（）

A、70分，70分 B、80分，80分 C、70分，80分 D、80分，70分

查看试题解析
8. 如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OA：OA′=2：3，则四边形ABCD与四边形A′B′C′D′的面积比为（）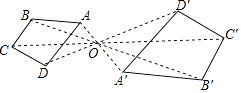

A、4：9 B、2：5 C、2：3 D、 $\sqrt{2}$ ： $\sqrt{3}$

查看试题解析
9. 已知x=3是分式方程 $\frac{k x}{x - 1}$ ﹣ $\frac{2 k - 1}{x}$ =2的解，那么实数k的值为（）

A、﹣1 B、0 C、1 D、2

查看试题解析
10. 在平面直角坐标系xOy中，二次函数y=ax²+bx+c的图象如图所示，下列说法正确的是（）

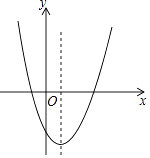A、abc＜0，b²﹣4ac＞0 B、abc＞0，b²﹣4ac＞0 C、abc＜0，b²﹣4ac＜0 D、abc＞0，b²﹣4ac＜0

查看试题解析

二、填空题

11. （ $\sqrt{2017}$ ﹣1）⁰= ．

查看试题解析
12. 在△ABC中，∠A：∠B：∠C=2：3：4，则∠A的度数为．

查看试题解析
13. 如图，正比例函数y₁=k₁x和一次函数y₂=k₂x+b的图象相交于点A（2，1），当x＜2时，y₁y₂ ．（填“＞”或“＜”）．

查看试题解析
14. 如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以M，N为圆心，以大于 $\frac{1}{2}$ MN的长为半径作弧，两弧相交于点P；③作AP射线，交边CD于点Q，若DQ=2QC，BC=3，则平行四边形ABCD周长为．

查看试题解析

三、解答题

15.

(1)、计算：| $\sqrt{2}$ ﹣1|﹣ $\sqrt{8}$ +2sin45°+（ $\frac{1}{2}$ ）^﹣²；

(2)、解不等式组： ${\begin{matrix} 2 x - 7 < 3 (x - 1) ① \\ \frac{4}{3} x + 3 \leq 1 - \frac{2}{3} x ② \end{matrix}$ ．

查看试题解析
16. 化简求值： $\frac{x - 1}{x^{2} + 2 x + 1}$ ÷（1﹣ $\frac{2}{x + 1}$ ），其中x= $\sqrt{3}$ ﹣1．

查看试题解析
17. 随着经济的快速发展，环境问题越来越受到人们的关注，某校学生会为了解节能减排、垃圾分类知识的普及情况，随机调查了部分学生，调查结果分为“非常了解”“了解”“了解较少”“不了解”四类，并将调查结果绘制成下面两个统计图．

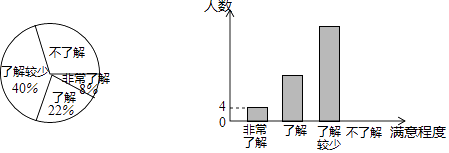(1)、本次调查的学生共有人，估计该校1200名学生中“不了解”的人数是人；

(2)、“非常了解”的4人有A₁ ， A₂两名男生，B₁ ， B₂两名女生，若从中随机抽取两人向全校做环保交流，请利用画树状图或列表的方法，求恰好抽到一男一女的概率．

查看试题解析
18. 科技改变生活，手机导航极大方便了人们的出行，如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60°方向行驶4千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B，C两地的距离．

查看试题解析
19. 如图，在平面直角坐标系xOy中，已知正比例函数y= $\frac{1}{2}$ x的图象与反比例函数y= $\frac{k}{x}$ 的图象交于A（a，﹣2），B两点．

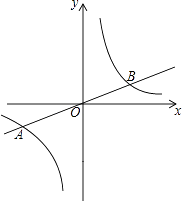(1)、求反比例函数的表达式和点B的坐标；

(2)、P是第一象限内反比例函数图象上一点，过点P作y轴的平行线，交直线AB于点C，连接PO，若△POC的面积为3，求点P的坐标．

查看试题解析
20. 如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．

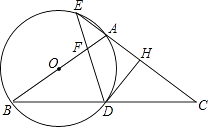(1)、求证：DH是圆O的切线；

(2)、若A为EH的中点，求 $\frac{E F}{F D}$ 的值；

(3)、若EA=EF=1，求圆O的半径．

查看试题解析

四、填空题

21. 如图，数轴上点A表示的实数是．

查看试题解析
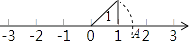22. 已知x₁ ， x₂是关于x的一元二次方程x²﹣5x+a=0的两个实数根，且x₁²﹣x₂²=10，则a= ．

查看试题解析
23. 已知⊙O的两条直径AC，BD互相垂直，分别以AB，BC，CD，DA为直径向外作半圆得到如图所示的图形，现随机地向该图形内掷一枚小针，记针尖落在阴影区域内的概率为P₁ ，针尖落在⊙O内的概率为P₂ ，则 $\frac{P_{1}}{P_{2}}$ = ．

查看试题解析
24. 在平面直角坐标系xOy中，对于不在坐标轴上的任意一点P（x，y），我们把点P′（ $\frac{1}{x}$ ， $\frac{1}{y}$ ）称为点P的“倒影点”，直线y=﹣x+1上有两点A，B，它们的倒影点A′，B′均在反比例函数y= $\frac{k}{x}$ 的图象上．若AB=2 $\sqrt{2}$ ，则k= ．

查看试题解析
25. 如图1，把一张正方形纸片对折得到长方形ABCD，再沿∠ADC的平分线DE折叠，如图2，点C落在点C′处，最后按图3所示方式折叠，使点A落在DE的中点A′处，折痕是FG，若原正方形纸片的边长为6cm，则FG=cm．

查看试题解析

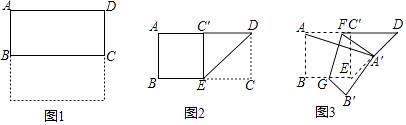
五、解答题

26. 随着地铁和共享单车的发展，“地铁+单车”已成为很多市民出行的选择，李华从文化宫站出发，先乘坐地铁，准备在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为x（单位：千米），乘坐地铁的时间y₁（单位：分钟）是关于x的一次函数，其关系如下表：
地铁站
A
B
C
D
E
x（千米）
8
9
10
11.5
13
y₁（分钟）
18
20
22
25
28

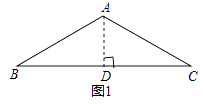
(1)、求y₁关于x的函数表达式；

(2)、李华骑单车的时间（单位：分钟）也受x的影响，其关系可以用y₂= $\frac{1}{2}$ x²﹣11x+78来描述，请问：李华应选择在那一站出地铁，才能使他从文化宫回到家所需的时间最短？并求出最短时间．

查看试题解析
27. 问题背景：如图1，等腰△ABC中，AB=AC，∠BAC=120°，作AD⊥BC于点D，则D为BC的中点，∠BAD= $\frac{1}{2}$ ∠BAC=60°，于是 $\frac{B C}{A B}$ = $\frac{2 B D}{A B}$ = $\sqrt{3}$ ；
迁移应用：如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠ADE=120°，D，E，C三点在同一条直线上，连接BD．

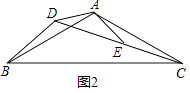(1)、①求证：△ADB≌△AEC；②请直接写出线段AD，BD，CD之间的等量关系式；

(2)、拓展延伸：如图3，在菱形ABCD中，∠ABC=120°，在∠ABC内作射线BM，作点C关于BM的对称点E，连接AE并延长交BM于点F，连接CE，CF．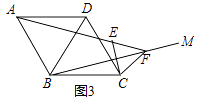
①证明△CEF是等边三角形；
②若AE=5，CE=2，求BF的长．

查看试题解析
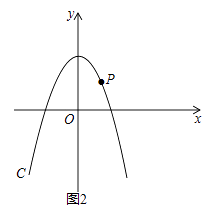
28.
如图1，在平面直角坐标系xOy中，抛物线C：y=ax²+bx+c与x轴相交于A，B两点，顶点为D（0，4），AB=4 $\sqrt{2}$ ，设点F（m，0）是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C′．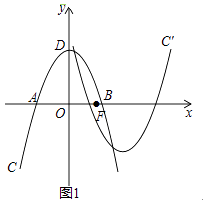

(1)、求抛物线C的函数表达式；

(2)、若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．

(3)、
如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．

查看试题解析

地铁站	A	B	C	D	E
x（千米）	8	9	10	11.5	13
y₁（分钟）	18	20	22	25	28

得分（分）	60	70	80	90	100
人数（人）	7	12	10	8	3