2017年山东省菏泽市中考数学试卷
试卷更新日期:2017-06-21 类型:中考真卷
一、选择题
-
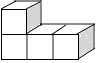
1. ( )﹣2的相反数是( )A、9 B、﹣9 C、 D、﹣2. 生物学家发现了一种病毒,其长度约为0.00000032mm,数据0.00000032用科学记数法表示正确的是( )A、3.2×107 B、3.2×108 C、3.2×10﹣7 D、3.2×10﹣83. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、
 B、
B、 C、
C、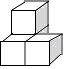 D、
D、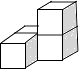 4. 某兴趣小组为了解我市气温变化情况,记录了今年1月份连续6天的最低气温(单位:℃):﹣7,﹣4,﹣2,1,﹣2,2.关于这组数据,下列结论不正确的是( )A、平均数是﹣2 B、中位数是﹣2 C、众数是﹣2 D、方差是75. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
4. 某兴趣小组为了解我市气温变化情况,记录了今年1月份连续6天的最低气温(单位:℃):﹣7,﹣4,﹣2,1,﹣2,2.关于这组数据,下列结论不正确的是( )A、平均数是﹣2 B、中位数是﹣2 C、众数是﹣2 D、方差是75. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( ) A、55° B、60° C、65° D、70°6. 如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x>ax+3的解集是( )
A、55° B、60° C、65° D、70°6. 如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x>ax+3的解集是( )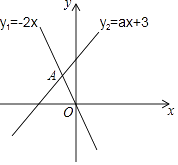 A、x>2 B、x<2 C、x>﹣1 D、x<﹣17. 如图,矩形ABOC的顶点A的坐标为(﹣4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是( )
A、x>2 B、x<2 C、x>﹣1 D、x<﹣17. 如图,矩形ABOC的顶点A的坐标为(﹣4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是( )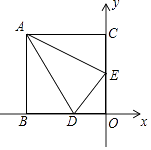 A、(0, ) B、(0, ) C、(0,2) D、(0, )8. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )
A、(0, ) B、(0, ) C、(0,2) D、(0, )8. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )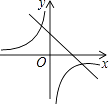 A、
A、 B、
B、 C、
C、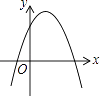 D、
D、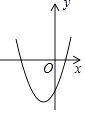
二、填空题
-
9. 分解因式:x3﹣x= .10. 关于x的一元二次方程(k﹣1)x2+6x+k2﹣k=0的一个根是0,则k的值是 .11. 菱形ABCD中,∠A=60°,其周长为24cm,则菱形的面积为 cm2 .12. 一个扇形的圆心角为100°,面积为15π cm2 , 则此扇形的半径长为 .13. 直线y=kx(k>0)与双曲线y= 交于A(x1 , y1)和B(x2 , y2)两点,则3x1y2﹣9x2y1的值为 .14. 如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=﹣ x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置,使点O1的对应点O2落在直线y=﹣ x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为 .
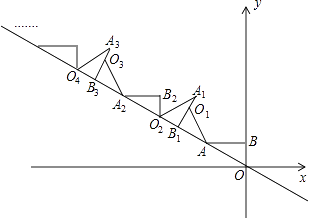
三、解答题
-
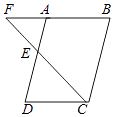
15. 计算:﹣12﹣|3﹣ |+2 sin45°﹣( ﹣1)2 .16. 先化简,再求值:(1+ )÷ ,其中x是不等式组 的整数解.17. 如图,E是▱ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.
 18. 如图,某小区①号楼与⑪号楼隔河相望,李明家住在①号楼,他很想知道⑪号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算⑪号楼的高度CD.
18. 如图,某小区①号楼与⑪号楼隔河相望,李明家住在①号楼,他很想知道⑪号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算⑪号楼的高度CD.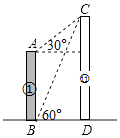 19. 列方程解应用题:
19. 列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
20. 如图,一次函数y=kx+b与反比例函数y= 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.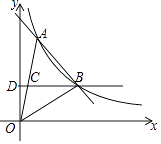 (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积.21. 今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了A、B、C、D四个等级,并绘制了如图不完整的扇形统计图和条形统计图.
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积.21. 今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了A、B、C、D四个等级,并绘制了如图不完整的扇形统计图和条形统计图.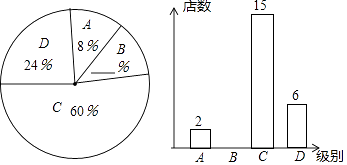
根据以上信息,解答下列问题:
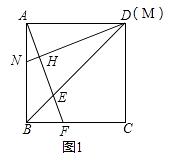
(1)、本次评估随即抽取了多少甲商业连锁店?(2)、请补充完整扇形统计图和条形统计图,并在图中标注相应数据;(3)、从A、B两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.22. 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.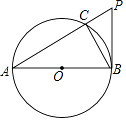 (1)、求证:∠BAC=∠CBP;(2)、求证:PB2=PC•PA;(3)、当AC=6,CP=3时,求sin∠PAB的值.23. 正方形ABCD的边长为6cm,点E、M分别是线段BD、AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.(1)、
(1)、求证:∠BAC=∠CBP;(2)、求证:PB2=PC•PA;(3)、当AC=6,CP=3时,求sin∠PAB的值.23. 正方形ABCD的边长为6cm,点E、M分别是线段BD、AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.(1)、如图1,若点M与点D重合,求证:AF=MN;
 (2)、
(2)、如图2,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以 cm/s的速度沿BD向点D运动,运动时间为t s.
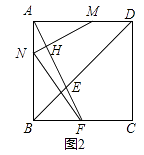
①设BF=y cm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.
24.如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3, ),过点D作DC⊥x轴,垂足为C.
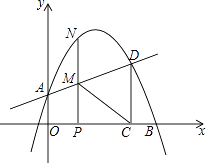 (1)、求抛物线的表达式;(2)、点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM面积的最大值;(3)、若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM面积的最大值;(3)、若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.