浙江省绍兴市越城区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-08-15 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列各图案中，是由一个基本图形通过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 已知空气的单位体积质量为1.24×10^﹣³克/厘米³ ， 1.24×10^﹣³用小数表示为（　　）

A、0.000124 B、0.0124 C、﹣0.00124 D、0.00124

查看试题解析
3. 下列四个多项式中，能因式分解的是（）

A、a²+1 B、a²﹣6a+9 C、x²+5y D、x²﹣5y

查看试题解析
4. 若3^x＝4，9^y＝7，则3^x^﹣^2y的值为（）

A、 $\frac{4}{7}$ B、 $\frac{7}{4}$ C、﹣3 D、 $\frac{2}{7}$

查看试题解析
5. 下列统计中，适合用“全面调查”的是（）

A、某厂生产的电灯使用寿命 B、全国初中生的视力情况 C、某校七年级学生的身高情况 D、“娃哈哈”产品的合格率

查看试题解析
6. 下列分式中不管x取何值，一定有意义的是（）

A、 $\frac{x^{2}}{x}$ B、 $\frac{x - 1}{x^{2} - 1}$ C、 $\frac{x + 3}{x^{2} + 1}$ D、 $\frac{x - 1}{x + 1}$

查看试题解析
7. 能使分式 $\frac{4 x + 7}{2 x - 3}$ 值为整数的整数x有（）个．

A、1 B、2 C、3 D、.4

查看试题解析
8. 2²⁰¹⁸﹣2²⁰¹⁹的值是（）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、﹣2²⁰¹⁸ D、﹣2

查看试题解析
9. 如图所示，把一根铁丝折成图示形状后，AB∥DE ，则∠BCD等于（）

A、∠D+∠B B、∠B﹣∠D C、180°+∠D﹣∠B D、180°+∠B﹣∠D

查看试题解析
10.
小明在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形如图（1）；小红看见了，说：“我也来试一试．”结果小红七拼八凑，拼成了如图（2）那样的正方形，中间还留下了一个洞，恰好是边长为3mm的小正方形，则每个小长方形的面积为（　　）

A、120mm² B、135mm² C、108mm² D、96mm²

查看试题解析

二、填空题（每小题3分，共24分

11. 当x＝时，分式 $\frac{x^{2} - 1}{(x + 3) (x - 1)}$ 的值是0．

查看试题解析
12. 当x²+kx+25是一个完全平方式，则k的值是．

查看试题解析
13. 若关于x的方程 $\frac{a x}{x - 1}$ ＝ $\frac{3}{x - 1}$ +1无解，则a的值是．

查看试题解析
14. 已知一组数据有40个，把它分成六组，第一组到第四组的频数分别是5，10，6，7，第五组的频率是0.2，故第六组的频数是．

查看试题解析
15. 3x+2y＝20的正整数解有．

查看试题解析
16. 如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝6，DH＝2，平移距离为3，则阴影部分的面积为．

查看试题解析
17. 已知m＝ $\frac{x - y}{x}$ 把公式变形成已知m ， y ，求x的等式．

查看试题解析
18. 一个自然数若能表示为相邻两个自然数的平方差，则这个自然数为“智慧数”，比如：2²﹣1²＝3，3就是智慧数，从0开始，不大于2019的智慧数共有个．

查看试题解析

三、解答题（共46分）

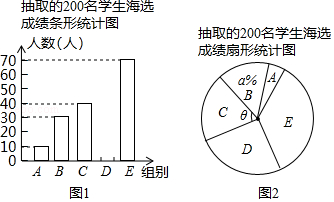
19. 化简

(1)、（﹣a²）³+3a²a⁴

(2)、 $\frac{a^{2}}{a - 1} - a - 1$

查看试题解析
20. 计算

(1)、 ${\begin{cases} x + 2 (x + 2 y) = 4 \\ x + 2 y = 2 \end{cases}$

(2)、 $\frac{2 x - 1}{x + 1} = 3$

查看试题解析
21. 化简 $\frac{x^{2} - 1}{x^{2} + 4 x + 4} \div (x + 1) \times \frac{x^{2} + 2 x}{x - 1}$ ，并在﹣2≤x≤2中选择适当的值代入求值．

查看试题解析
22. 师生对话，师：我像你这么大的时候，你才1岁，你到我这样大的时候，我已经40岁了，问老师和学生现在各几岁？

查看试题解析

23. 中华文明，源远流长：中华诗词，寓意深广．为了传承优秀传统文化，我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次海选比赛的成绩分布情况，随机抽取了其中200名学生的海选比赛成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列统计图表

组别	海选成绩x
A组	50≤x＜60
B组	60≤x＜70
C组	70≤x＜80
D组	80≤x＜90
E组	90≤x＜100

请根据所给信息，解答下列问题

(1)、图1条形统计图中D组人数有多少？

(2)、在图2的扇形统计图中，记表示B组人数所占的百分比为a%，则a的值为，表示C组扇形的圆心角的度数为度；

(3)、规定海选成绩在90分以上（包括90分）记为“优等”，请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人？

查看试题解析

24. 杨辉三角形，又称贾宪三角形，帕斯卡三角形，是二项式系数在三角形中的一种几何排列，在我国南宋数学家杨所著的《详解九章算术》（1261年）一书中用如图的三角形解释二项和的乘方规律
（a+b）¹＝a+b

（a+b）²＝a²+2ab+b²

（a+b）³＝（a+b）（a²+2ab+b²）＝a³+3a²b+3ab²+b³

（a+b）⁴＝（a+b）（a³+3a²b+3ab²+b³）＝a⁴+4a³b+6a²b²+4ab³+b⁴

“杨辉三角”里面蕴藏了许多的规律

(1)、找出其中各项字母之间的规律以及各项系数之间的规律各一条；

(2)、直接写出（a+b）⁶展开后的多项式；

(3)、运用：若今天是星期四，经过8⁴天后是星期，经过8¹⁰⁰天后是星期．

查看试题解析
25. 如图为一台灯示意图，其中灯头连接杆DE始终和桌面FG平行，灯脚AB始终和桌面FG垂直，

(1)、当∠EDC＝∠DCB＝120°时，求∠CBA；

(2)、连杆BC、CD可以绕着B、C和D进行旋转，灯头E始终在D左侧，设∠EDC ， ∠DCB ， ∠CBA的度数分别为α，β，γ，请画出示意图，并直接写出示意图中α，β，γ之间的数量关系．

查看试题解析