浙江省宁波市鄞州区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-08-15 类型:期末考试
一、选择题(每小题3分,共30分)
-
1. 正方形的一个内角度数是A、 B、 C、 D、2. 下列计算正确的是A、 B、 C、 D、3. 在某人才招聘会上,组办方对应聘者进行了“听、说、读、写”四项技能测试,若人才要求是具有强的“听”力,较强的“说与“读“能力及基本的“写”能力,根据这个要求,听、说、读、写”四项技能测试比较合适的权重设计是A、 B、 C、 D、4. 若关于 的一元二次方程 通过配方法可以化成 的形式,则 的值不可能是A、3 B、6 C、9 D、105. 在平面直角坐标系中,矩形 的顶点 , , 的坐标分别为 , , ,则顶点 的坐标是A、 B、 C、 D、6. 利用反证法证明命题“在 中,若 ,则 ”时,应假设 )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 已知反比例函数 ,当 时,自变量 的取值范围是A、 B、 C、 D、 或8. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、 B、
B、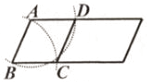 C、
C、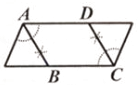 D、
D、 9. 如图,在四边形 中, , , , , .若点 , 分别是边 , 的中点,则 的长是
9. 如图,在四边形 中, , , , , .若点 , 分别是边 , 的中点,则 的长是 A、 B、 C、2 D、10. 如图, 的一边 在 轴上,长为5,且 ,反比例函数 和 分别经过点 , ,则 的周长为
A、 B、 C、2 D、10. 如图, 的一边 在 轴上,长为5,且 ,反比例函数 和 分别经过点 , ,则 的周长为 A、12 B、14 C、 D、
A、12 B、14 C、 D、二、填空题(每小题3分,共18分)
-
11. 式子 在实数范围内有意义,则x的取值范围是 .
12. 从一个多边形的一个顶点出发可以引5条对角线,这个多边形的边数是 .13. 若 是一元二次方程 的解,则代数式 的值是14. 小明利用公式 计算5个数据的方差,则这5个数据的标准差 的值是 .15. 如图,菱形 中, ,点 是直线 上的一点.已知 的面积为6,则线段 的长是 . 16. 如图,矩形 中, , ,点 是矩形 的边 上的一动点,以 为边,在 的右侧构造正方形 ,连结 ,则 的最小值为 .
16. 如图,矩形 中, , ,点 是矩形 的边 上的一动点,以 为边,在 的右侧构造正方形 ,连结 ,则 的最小值为 .
三、解答题(第17-23题各6分,第24题10分,共52分)
-
17. 计算:(1)、(2)、18. 解方程:(1)、(2)、19. 某校八年级两个班各选派10名学生参加“垃圾分类知识竞赛,各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下
班级
最高分
平均分
中位数
众数
方差
八(1)班
100
93
93
12
八(2)班
99
95
8.4
(1)、求表中 , , 的值;(2)、依据数据分析表,有同学认为最高分在(1)班,(1)班的成绩比(2)班好.但也有同学认为(2)班的成绩更好.请你写出两条支持八(2)班成绩更好的理由.20. 如图,正比例函数 的图象与反比例函数 的图象交于 , 两点,其中点 的横坐标为 .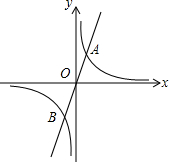 (1)、求 的值.(2)、若点 是 轴上一点,且 ,求点 的坐标.21. 如图,矩形 中, , ,过对角线 的中点 的直线分别交 , 边于点 , 连结 , .
(1)、求 的值.(2)、若点 是 轴上一点,且 ,求点 的坐标.21. 如图,矩形 中, , ,过对角线 的中点 的直线分别交 , 边于点 , 连结 , . (1)、求证:四边形 是平行四边形.(2)、当四边形 是菱形时,求 及 的长.22. 一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.(1)、若将这种水果每千克的售价降低 元,则每天销售量是多少千克?(结果用含 的代数式表示)(2)、若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?23. 小林为探索函数 的图象与性经历了如下过程
(1)、求证:四边形 是平行四边形.(2)、当四边形 是菱形时,求 及 的长.22. 一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.(1)、若将这种水果每千克的售价降低 元,则每天销售量是多少千克?(结果用含 的代数式表示)(2)、若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?23. 小林为探索函数 的图象与性经历了如下过程 (1)、列表:根据表中 的取值,求出对应的 值,将空白处填写完整
(1)、列表:根据表中 的取值,求出对应的 值,将空白处填写完整2.5
3
3.5
4
4.5
5
6
2
1.2
1
(2)、以表中各组对应值为点的坐标,在平面直角坐标系中描点并画出函数图象.(3)、若函数 的图象与 的图象交于点 , ,且 为正整数),则 的值是 .24. 定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线 ,点 , 在直线 上,点 , 在直线 上,若 ,则四边形 是半对角四边形. (1)、如图1,已知 , , ,若直线 , 之间的距离为 ,则 的长是 , 的长是;(2)、如图2,点 是矩形 的边 上一点, , .若四边形 为半对角四边形,求 的长;(3)、如图3,以 的顶点 为坐标原点,边 所在直线为 轴,对角线 所在直线为 轴,建立平面直角坐标系.点 是边 上一点,满足 .
(1)、如图1,已知 , , ,若直线 , 之间的距离为 ,则 的长是 , 的长是;(2)、如图2,点 是矩形 的边 上一点, , .若四边形 为半对角四边形,求 的长;(3)、如图3,以 的顶点 为坐标原点,边 所在直线为 轴,对角线 所在直线为 轴,建立平面直角坐标系.点 是边 上一点,满足 .①求证:四边形 是半对角四边形;
②当 , 时,将四边形 向右平移 个单位后,恰有两个顶点落在反比例函数 的图象上,求 的值.