广西南宁市马山县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-08-15 类型：期末考试

进入出卷网下载

一、选择题（共12小题，每小題3分，共36分.）

1. π的相反数是（）

A、π B、一π C、 $\frac{1}{π}$ D、﹣ $\frac{1}{π}$

查看试题解析
2. 海关总署5月8日公布中国进口数据显示，今年前4个月我国货物贸易进出口总值9 510 000 000 000元，其中数据9 510 000 000 000科学记数法表示是（）

A、95.1×10¹¹ B、9.51×10¹² C、0.951×10¹³ D、951×10¹⁰

查看试题解析
3. 下列各项调查中，最适合用全面调查（普查）的是（）

A、了解国内外观众对电影《流浪地球》的观影感受 B、了解太原市九年级学生每日睡眠时长 C、“长征﹣3B火箭”发射前，检查其各零部件的合格情况 D、检测一批新出厂的手机的使用寿命

查看试题解析
4. 不等式x﹣3≥﹣1的解集是（）

A、x≤2 B、x＝﹣2 C、x≥2 D、x≥﹣2

查看试题解析
5. 在方程组 ${\begin{cases} 3 x + y = 7 ① \\ y = x - 1 ② \end{cases}$ 中，把②代入①，得（）

A、3x﹣x+1＝7 B、3x+x+1＝7 C、3x﹣1＝7 D、3x+x﹣1＝7

查看试题解析
6. 下列各式计算正确的是（）

A、（﹣2）³＝﹣8 B、 $\sqrt[3]{- 8}$ ＝2 C、﹣3²＝9 D、 $\sqrt{9}$ ＝±3

查看试题解析
7. 如图，直线a∥b，将三角尺的直角顶点放在直线b上，若∠1＝35°，则∠2等于（）

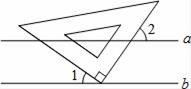A、45° B、55° C、35° D、65°

查看试题解析
8. 下列命题是真命题的是（）

A、相等的角是对顶角 B、互补的两个角一定是邻补角 C、如果a＝b，那么a²＝b² D、如果两个角是同位角，那么这两个角一定相等

查看试题解析
9. 如图，点D是锐角三角形ABC的边BC上一个动点，当点D从B向C运动时，AD的长度（）

A、变大 B、变小 C、先变大然后变小 D、先变小而后变大

查看试题解析
10. 一个正数的平方根是2m+3和m+1，则这个数为（）

A、﹣ $\frac{4}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{9}$ D、1或 $\frac{1}{9}$

查看试题解析
11. 小颖家离学校1200米，其中有一段为上坡路，另一段为下坡路．她去学校共用了16分钟．假设小颖上坡路的平均速度是3千米/时，下坡路的平均速度是5千米/时．若设小颖上坡用了x分钟，下坡用了y分钟，根据题意可列方程组为（）

A、 $\{\begin{cases} 3 x + 5 y = 1200 \\ x + y = 16 \end{cases}$ B、 $\{\begin{cases} \frac{3}{60} x + \frac{5}{60} y = 1.2 \\ x + y = 16 \end{cases}$ C、 $\{\begin{cases} 3 x + 5 y = 1.2 \\ x + y = 16 \end{cases}$ D、 $\{\begin{cases} \frac{3}{60} x + \frac{5}{60} y = 1200 \\ x + y = 16 \end{cases}$

查看试题解析
12. 定义[x]为不超过x的最大整数，如[3.6]＝3，[0.6]＝0，[﹣3.6]＝﹣4，对于任意实数x下列式子中成立的是（）

A、[x]＝x B、0≤x﹣[x]＜1 C、[x+y]≤[x]+[y] D、[n+x]＝n+[x]

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分

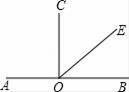
13. 某中学八年级共有900名学生，为了解该校八年级学生每天做家庭作业所用的时间，从该校八年级学生中随机抽取100名学生进行调查，此次调查的样本容量是．

查看试题解析
14. 若 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是关于 $x$ ， $y$ 的二元一次方程 $3 x + m y = 10$ 的解，则 $m$ =.

查看试题解析
15. 如图，OC⊥AB，OE为∠COB的平分线，∠AOE的度数为度．

查看试题解析
16. 在平面直角坐标系中，已知点A（m﹣1，m+4）在第二象限，则m的取值范围是．

查看试题解析
17. 如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2）．把一条长为2019个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是．

查看试题解析

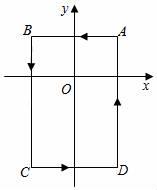
三、解答题：本大题共8小题，共66分

18. 计算：（﹣2）² $\div \frac{2}{3}$ ﹣| $\sqrt{3} - 1$ |﹣ $\sqrt{3}$ ．

查看试题解析
19. 解方程组： ${\begin{cases} x + 2 y = 31 \\ 2 x - y = 12 \end{cases}$ ．

查看试题解析
20. 解不等式组 ${\begin{cases} 2 x - 1 < 5 \\ 3 x + 6 \geq 0 \end{cases}$ 并把解集在数轴上表示出来．

查看试题解析
21. 如图，在边长为1个单位长度的小正方形组成的网格中．

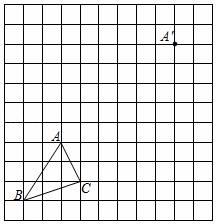(1)、画图：平移三角形ABC至三角形A′B′C′，使点A与A′对应．

(2)、线段AB与A′B′的位置关系是．

(3)、求△ABC的面积．

查看试题解析
22. 为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料的人数是40人．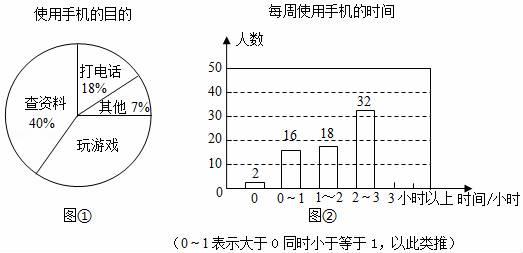

请你根据以上信息解答下列问题：

(1)、在扇形统计图中，“玩游戏对应的百分比为，圆心角度数是度．

(2)、补全条形统计图；

(3)、该校共有学生2100人，估计每周使用手机时间在2小时以上（不含2小时）的人数．

查看试题解析
23. 如图，AD平分∠BDC，∠1＝∠2，∠B+∠F＝180°．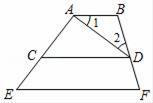

(1)、写出3个∠B的同旁内角；

(2)、若∠B＝105°，求∠ADC的度数．

(3)、求证：CD∥EF．

查看试题解析
24. 快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣．已知购买甲型机器人1台，乙型机器人2台，共需14万元；购买甲型机器人2台，乙型机器人3台，共需24万元．

(1)、求甲、乙两种型号的机器人每台的价格各是多少万元；

(2)、已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件，该公司计划最多用41万元购买8台这两种型号的机器人，则该公司该如何购买，才能使得每小时的分拣量最大？

查看试题解析
25. 如图1在平面直角坐标系中，线段AB的两个端点坐标分别为A（0，2），B（﹣1，0），将线段AB向右平移3个单位长度，得到线段CD，连接AD．

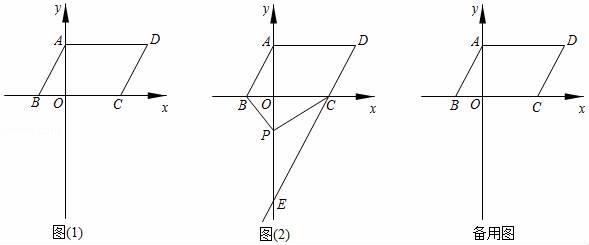(1)、直接写出点C、点D的坐标．

(2)、如图2延长DC交y轴于点E，点P是线段OE上的一个动点，连接BP、CP猜想∠ABP、∠BPC、∠ECP之间的数量关系，并说明理由．

(3)、在坐标轴上是否存在点Q使三角形QBD的面积与四边形ABCD的面积相等？若存在，请直接写出坐标；若不存在，试说明理由．

查看试题解析