广西南宁市马山县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-08-15 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分.)
-
1. 将下列长度的三根木棒首尾顺次连接, 能组成直角三角形的是 ( )
A、1、2、3 B、2、3、4 C、3、4、5 D、4、5、62. 下列函数中,一定是一次函数的是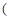
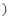 A、
A、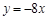 B、
B、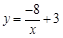 C、
C、 D、
D、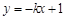 3. 下列二次根式中,最简二次根式为
3. 下列二次根式中,最简二次根式为
 A、
A、 B、
B、 C、
D、
C、
D、 4. 一组数据2,2,4,3,6,5,2的众数和中位数分别是
4. 一组数据2,2,4,3,6,5,2的众数和中位数分别是
 A、3,2 B、2,3 C、2,2 D、2,45. 下列图象不能反映 y 是
A、3,2 B、2,3 C、2,2 D、2,45. 下列图象不能反映 y 是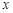 的函数的是
的函数的是 
 A、
A、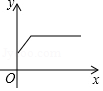 B、
B、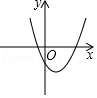 C、
C、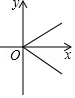 D、
D、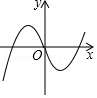 6. 如图,在
6. 如图,在 中,点
中,点 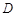 、
、 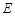 分别是
分别是  、
、  的中点,如果
的中点,如果  ,那么
,那么  的长为
的长为 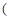
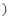
 A、4 B、5 C、6 D、77. 如图,将
A、4 B、5 C、6 D、77. 如图,将 的一边
的一边  延长至点
延长至点 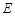 ,若
,若  ,则
,则  等于
等于 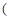
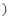
 A、
A、 B、
B、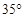 C、
C、 D、
D、 8. 下列计算正确的是
8. 下列计算正确的是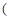
 A、
A、 B、
B、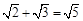 C、
C、 D、
D、 9. 某中学随机调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
9. 某中学随机调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:时间
 小时
小时5
6
7
8
人数
10
10
20
10
则这50名学生这一周在校的平均体育锻炼时间是
 A、6.2小时 B、6.5小时 C、6.6小时 D、7小时10. 如图, 矩形 ABCD 的对角线 ,
A、6.2小时 B、6.5小时 C、6.6小时 D、7小时10. 如图, 矩形 ABCD 的对角线 , 交于点 ,
交于点 ,  ,
,  ,则
,则  的长为 ( )
的长为 ( ) A、4cm B、4cm C、2cm D、2cm11. 已知:如图,菱形
A、4cm B、4cm C、2cm D、2cm11. 已知:如图,菱形 中,对角线
中,对角线  、
、 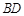 相交于点
相交于点  ,且
,且  ,
, 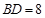 ,点
,点 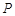 是线段
是线段  上任意一点,且
上任意一点,且  ,垂足为
,垂足为 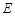 ,
,  ,垂足为
,垂足为  ,则
,则  的值是
的值是 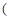
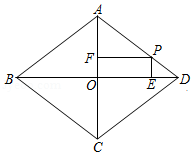 A、12 B、24 C、36 D、4812. 如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用
A、12 B、24 C、36 D、4812. 如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用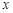 , y 表示直角三角形的两直角边
, y 表示直角三角形的两直角边  ,下列四个说法:①
,下列四个说法:①  ;②
;②  ;③
;③  ;④
;④  ;其中说法正确的是
;其中说法正确的是 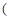
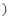
 A、①② B、①②③ C、①②④ D、①②③④
A、①② B、①②③ C、①②④ D、①②③④二、填空题(本大题共6小题,每小题3分,共18分.)
-
13. 要使二次根式
 有意义,则自变量
有意义,则自变量 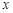 的取值范围是 . 14. 现有甲、乙两支足球队,每支球队队员身高的平均数均为1.85米,方差分别为
的取值范围是 . 14. 现有甲、乙两支足球队,每支球队队员身高的平均数均为1.85米,方差分别为 ,
,  ,则身高较整齐的球队是队 15. 每本书的厚度为
,则身高较整齐的球队是队 15. 每本书的厚度为 ,把这些书摞在一起总厚度 y (单位:
,把这些书摞在一起总厚度 y (单位:  随书的本数
随书的本数 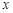 的变化而变化,请写出 y 关于
的变化而变化,请写出 y 关于 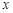 的函数解析式 , (不用写自变量的取值范围) 16. 如图,在菱形
的函数解析式 , (不用写自变量的取值范围) 16. 如图,在菱形 中,点
中,点 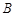 在
在 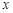 轴上,点
轴上,点 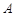 的坐标为
的坐标为  ,则点
,则点  的坐标为 .
的坐标为 .  17. 一次函数
17. 一次函数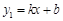 与
与  的图象如图,则
的图象如图,则 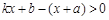 的解集是 .
的解集是 . 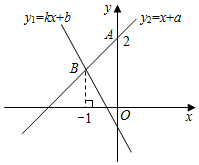 18. 将2019个边长都为
18. 将2019个边长都为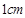 的正方形按如图所示的方法摆放,点
的正方形按如图所示的方法摆放,点  ,
,  ,
,  分别是正方形对角线的交点,则2019个正方形重叠形成的重叠部分的面积和为
分别是正方形对角线的交点,则2019个正方形重叠形成的重叠部分的面积和为 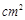 .
. 
三、解答题(本大题共8小题,共66分.)
-
19. 计算:
 20. 已知:
20. 已知: ,
, 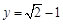 ,求
,求  的值. 21. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
的值. 21. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:完成作业
单元测试
期末考试
小张
70
90
80
小王
60
75
(1)、若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;(2)、若按完成作业、单元检测、期末考试三项成绩按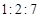 的权重来确定期末评价成绩.
的权重来确定期末评价成绩. ①请计算小张的期末评价成绩为多少分?
②小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
22. 如图,在平行四边形 中,点
中,点 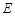 、
、  别在
别在  ,
,  上,且
上,且  .
.  (1)、如图①,求证:四边形
(1)、如图①,求证:四边形 是平行四边形;
(2)、如图②,若
是平行四边形;
(2)、如图②,若 ,且
,且  .
.  ,求平行四边形
,求平行四边形  的周长.
23. 如图,某校组织学生到
的周长.
23. 如图,某校组织学生到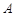 地开展社会实践活动,乘车到达
地开展社会实践活动,乘车到达 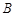 地后,发现
地后,发现 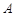 地恰好在
地恰好在 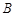 地的正北方向,导航显示车辆应沿北偏东
地的正北方向,导航显示车辆应沿北偏东  方向行驶10公里到达
方向行驶10公里到达 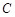 地,再沿北偏西
地,再沿北偏西  方向行驶一段距离才能到达
方向行驶一段距离才能到达 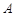 地.求
地.求 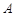 、
、 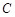 两地间的距离,
两地间的距离,  24. 甲乙两人同时登山,甲乙两人距地面的高度
24. 甲乙两人同时登山,甲乙两人距地面的高度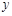 (米
(米 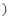 与登山时间
与登山时间  (分
(分 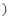 之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:  (1)、甲登山的速度是米
(1)、甲登山的速度是米 分钟,乙在
分钟,乙在 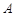 地提速时距地面的高度
地提速时距地面的高度  为米; (2)、直接写出甲距地面高度
为米; (2)、直接写出甲距地面高度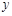 (米
(米 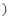 和
和  (分
(分  之间的函数关系式; (3)、若乙提速后,乙的速度是甲登山速度的3倍.请问登山多长时间时,乙追上了甲,此时乙距
之间的函数关系式; (3)、若乙提速后,乙的速度是甲登山速度的3倍.请问登山多长时间时,乙追上了甲,此时乙距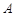 地的高度为多少米? 25. 如图,在四边形
地的高度为多少米? 25. 如图,在四边形 中,
中, 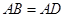 ,
, 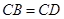 , 是 上一点,
, 是 上一点,  交
交  于点 ,连结
于点 ,连结  .
.  (1)、求证:
(1)、求证: ; (2)、若
; (2)、若 ,试说明四边形
,试说明四边形  是菱形; (3)、在(2)的条件下,试确定 点的位置,使得
是菱形; (3)、在(2)的条件下,试确定 点的位置,使得 ,并说明理由. 26.
,并说明理由. 26.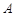 村有肥料200吨,
村有肥料200吨, 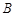 村有肥料300吨,现要将这些肥料全部运往
村有肥料300吨,现要将这些肥料全部运往 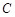 、
、 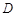 两仓库.从
两仓库.从 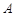 村往
村往 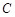 、
、 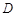 两仓库运肥料的费用分别为每吨20元和25元;从
两仓库运肥料的费用分别为每吨20元和25元;从 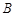 村往
村往 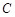 、
、 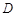 两仓库运肥料的费用分别为每吨15元和18元;现
两仓库运肥料的费用分别为每吨15元和18元;现 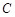 仓库需要肥料240吨,现
仓库需要肥料240吨,现 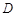 仓库需要肥料260吨.
(1)、设
仓库需要肥料260吨.
(1)、设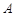 村运往
村运往 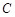 仓库
仓库  吨肥料,
吨肥料, 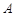 村运肥料需要的费用为
村运肥料需要的费用为  元;
元; 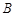 村运肥料需要的费用为
村运肥料需要的费用为  元.
元. ①写出
 、
、  与
与  的函数关系式,并求出
的函数关系式,并求出  的取值范围;
的取值范围;②试讨论
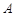 、
、 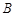 两村中,哪个村的运费较少?(2)、考虑到
两村中,哪个村的运费较少?(2)、考虑到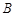 村的经济承受能力,
村的经济承受能力, 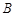 村的运输费用不得超过4830元,设两村的总运费为
村的运输费用不得超过4830元,设两村的总运费为  元,怎样调运可使总运费最少?
元,怎样调运可使总运费最少?