广西岑溪市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期：2019-08-15 类型：期末考试
一、选择题（本大题共12小题；每小题3分，共36分.）
-
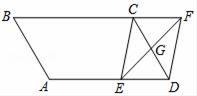
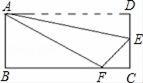
1. 在下列数据6，5，7，5，8，6，6中，众数是（ ）A、5 B、6 C、7 D、82. 下列式子中为最简二次根式的是（ ）A、 B、 C、 D、3. 下列运算正确的是（ ）A、 ﹣ ＝ B、 + ＝4 C、 ＝3 D、 × ＝4. 以下列各组线段为边，能构成直角三角形的是（ ）A、1cm，2cm，3cm B、 cm， cm，5cm C、6cm，8cm，10cm D、5cm，12cm，18cm5. 下列条件中，不能判定一个四边形是平行四边形的是（ ）A、两组对边分别平行 B、一组对边平行且相等 C、一组对边相等且一组对角相等 D、两组对角分别相等6. 用配方法解方程x2+8x+7=0，则配方正确的是（ ）A、（x+4）2=9 B、（x﹣4）2=9 C、（x﹣8）2=16 D、（x+8）2=577. 12名同学参加了学校组织的经典诵读比赛的个人赛（12名同学成绩各不相同），按成绩取前6名进入决赛，如果小明知道自己的成绩后，要判断自己能否进入决赛，他需要知道这12名同学成绩的（ ）A、 方差 B、平均数 C、众数 D、中位数8. 已知关于x的一元二次方程x2+2x+k＝0有实数根，则k的取值范围是（ ）A、k≤1 B、k≥1 C、k＜1 D、k＞19. 如图，矩形ABCD边AD沿折痕AE折叠，使点D落在BC上的F处，已知AB＝6，△ABF的面积是24，则FC等于（ ）
A、1 B、2 C、3 D、410.如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（ ）
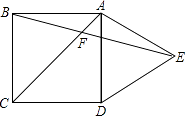A、45° B、55° C、60° D、75°11. 如图所示，有一个高18cm，底面周长为24cm的圆柱形玻璃容器，在外侧距下底1cm的点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇，则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是（ ）
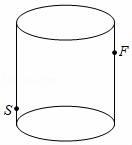A、16cm B、18cm C、20cm D、24cm二、填空题（每小题3分，共18分）
-
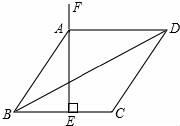
12. = ．13. 已知直角三角形的两边长为3、4，则另一条边长是 ．14. 一个多边形的外角和是内角和的 倍，这个多边形的边数是 ．15. 某中学组织初二学生开展篮球比赛，以班为单位单循环形式（每两班之间赛一场），现计划安排15场比赛，则共有多少个班级参赛？设有x个班级参赛，根据题意，可列方程为 ．16. 一组数据：5，8，7，6，9，则这组数据的方差是 ．17. 如图，菱形ABCD的周长为16cm，BC的垂直平分线EF经过点A，则对角线BD长为cm．
三、解答题（本大题共7小题，共46分.）
-
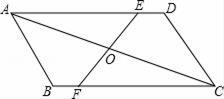
18. 计算： ÷ ﹣ × + ．19. 解方程：3（x﹣7）＝4x（x﹣7）20. 如图，在平行四边形ABCD中，过AC中点O作直线，分别交AD、BC于点E、F．
求证：△AOE≌△COF．
21. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫格点，网格中有以格点A、B、C为顶点的△ABC，请你根据所学的知识回答下列问题：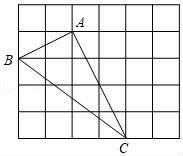
(1)、求△ABC的面积；(2)、判断△ABC的形状，并说明理由．22. 我市提倡“诵读中华经典，营造书香校园”的良好诵读氛围，促进校园文化建设，进而培养学生的良好诵读习惯，使经典之风浸漫校园．某中学为了了解学生每周在校经典诵读时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表，请根据图表信息解答下列问题：时间（小时）
频数（人数）
频率
2≤t＜3
4
0.1
3≤t＜4
10
0.25
4≤t＜5
a
0.15
5≤t＜6
8
b
6≤t＜7
12
0.3
合计
40
1
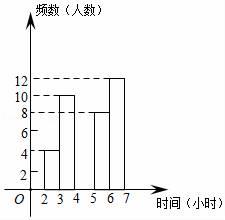(1)、表中的a＝ ， b＝；(2)、请将频数分布直方图补全；(3)、若该校共有1200名学生，试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名？
