2016-2017学年河北省唐山市玉田县高一下学期期中数学试卷

试卷更新日期：2017-06-21 类型：期中考试

进入出卷网下载

一、选择题

1. 等差数列{a_n}中，前n项的和为S_n ，若a₇=1，a₉=5，那么S₁₅等于（）

A、90 B、45 C、30 D、 $\frac{45}{2}$

查看试题解析
2. 如果a＜b＜0，那么下列不等式成立的是（）

A、 $\frac{1}{a} < \frac{1}{b}$ B、ab＜b² C、ac²＜bc² D、|a|＞|b|

查看试题解析
3. 数列{a_n}满足a₁=2，a_n₊₁= $\frac{1}{1 - a_{n}} (n \in N^{+})$ ，则a₂₀₁₇=（）

A、﹣2 B、﹣1 C、2 D、 $\frac{1}{2}$

查看试题解析
4. 数列{a_n}中，对任意n∈N^* ， a₁+a₂+…+a_n=2ⁿ﹣1，则a₁²+a₂²+…+a_n²等于（）

A、（2ⁿ﹣1）² B、 $\frac{{(2^{n} - 1)}^{2}}{3}$ C、4ⁿ﹣1 D、 $\frac{4^{n} - 1}{3}$

查看试题解析
5. △ABC的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且c=2a，则cosB=（　　）

A、 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{\sqrt{2}}{3}$

查看试题解析
6. 设x，y满足约束条件 ${\begin{cases} x + y - 7 \leq 0 \\ x - 3 y + 1 \leq 0 \\ 3 x - y - 5 \geq 0 \end{cases}$ ，则z=2x﹣y的最大值为（）

A、10 B、8 C、3 D、2

查看试题解析
7. 在△ABC中，若 $\frac{\tan A}{\tan B} = \frac{a^{2}}{b^{2}}$ ，则△ABC的形状是（）

A、直角三角形 B、等腰或直角三角形 C、不能确定 D、等腰三角形

查看试题解析
8. 设S_n为等差数列{a_n}的前n项和，若a₅＞0，a₁+a₁₀＜0，则当S_n最大时正整数n为（）

A、4 B、5 C、6 D、10

查看试题解析
9. 不等式x²﹣4x＞2ax+a对一切实数x都成立，则实数a的取值范围是（）

A、（1，4） B、（﹣4，﹣1） C、（﹣∞，﹣4）∪（﹣1，+∞） D、（﹣∞，1）∪（4，+∞）

查看试题解析
10. 设S_n是等比数列{a_n}的前n项和，S₄=5S₂ ，则此数列的公比q=（）

A、﹣2或﹣1 B、1或2 C、±1或2 D、±2或﹣1

查看试题解析
11. 在△ABC中，角A、B、C所对的边分别为a、b、c．若c=3， $C = \frac{π}{3}$ ，且a+b=4，则△ABC的面积为（）

A、 $\frac{7 \sqrt{3}}{12}$ B、 $\frac{7 \sqrt{3}}{4}$ C、 $\frac{7}{12}$ D、 $\frac{5 \sqrt{3}}{12}$

查看试题解析
12. 若正数x，y满足x+3y=xy，则3x+4y的最小值为（）

A、24 B、25 C、28 D、30

查看试题解析

二、填空题：本大题共4小题，把答案填在答题卷的横线上..

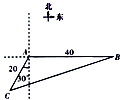
13. 设S_n是等差数列{a_n}的前n项和，若S₃=﹣3，S₇=7，则S₅= ．

查看试题解析
14. 若△ABC的内角A，B，C的对边分别为a，b，c，若a+b=2，∠C=120°，则边c的最小值是．

查看试题解析
15. 如图，位于A处的海面观测站获悉，在其正东方向相距40海里的B处有一艘渔船遇险，并在原地等待营救．在A处南偏西30°且相距20海里的C处有一艘救援船，该船接到观测站通告后立即前往B处求助，则sin∠ACB= ．

查看试题解析
16. 已知等比数列{a_n}中，a₂=1，则其前三项和S₃的取值范围是．

查看试题解析

三、解答题：

17. 等差数列{a_n}的前n项和为S_n ，且a₃+a₅=a₄+7，S₁₀=100．

(1)、求{a_n}的通项公式；

(2)、求满足不等式S_n＜3a_n﹣2的n的值．

查看试题解析
18. 若△ABC的内角A，B，C的对边分别为a，b，c，已知c=2，C= $\frac{π}{3}$ ．

(1)、若b= $\frac{2 \sqrt{6}}{3}$ ，求角B；

(2)、若sinC+sin（B﹣A）=2sin2A，求△ABC的面积．

查看试题解析
19. 设数列{a_n}的前n项和为S_n ，已知S₂=4，a_n₊₁=2S_n+1，n∈N^* ．

(1)、求通项公式a_n；

(2)、求数列{|a_n﹣n﹣2|}的前n项和．

查看试题解析
20. 在△ABC中，角A，B，C所对的边分别为a，b，c，且 $\sqrt{2}$ asinA=（ $\sqrt{2}$ b﹣c）sinB+（ $\sqrt{2}$ c﹣b）sinC．

(1)、求角A的大小；

(2)、若a= $\sqrt{10}$ ，cosB= $\frac{2 \sqrt{5}}{5}$ ，D为AC的中点，求BD的长．

查看试题解析
21. 某客运公司用A，B两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次．A，B两种车辆的载客量分别为36人和60人，在甲地和乙地之间往返一次的营运成本分别为1600元/辆和2400元/辆．公司拟组建一个不超过21辆车的客运车队，并要求B型车不多于A型车7辆．若每天要运送不少于900人从甲地去乙地的旅客，并于当天返回，为使公司从甲地去乙地的营运成本最小，那么应配备A型车、B型车各多少辆？营运成本最小为多少元？

查看试题解析
22. 在等比数列{a_n}中，a₁=2，a₃ ， a₂+a₄ ， a₅成等差数列．

(1)、求数列{a_n}的通项公式

(2)、若数列{b_n}满足b₁+ $\frac{b_{2}}{2}$ +…+ $\frac{b_{n}}{n}$ =a_n（n∈N^*），{b_n}的前n项和为S_n ，求使S_n﹣na_n+6≥0成立的正整数n的最大值．

查看试题解析