吉林省长春市汽开区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-08-15 类型：期中考试
一、单选题
-
1. 计算（﹣a）2•a3的结果是（ ）A、a5 B、a6 C、﹣a5 D、﹣a62. 下列运算正确的是（ ）A、（a+1）2=a2+1 B、3ab2c÷a2b=3ab C、（﹣2ab2）3=8a3b6 D、x3•x=x43. 要测量圆形工件的外径，工人师傅设计了如右图所示的卡钳，O为卡钳两柄交点，且有OA=OB=OC=OD，如果圆形工件恰好通过卡钳AB，则这个工件的外径必是CD之长了，其中的依据是全等三角形的判定条件（ ）
A、ASA B、AAS C、SAS D、SSS4. 若（x+m）（x﹣8）中不含x的一次项，则m的值为（ ）A、8 B、﹣8 C、0 D、8或﹣85. 我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图甲可以用来解释（a+b）2﹣（a﹣b）2=4a B．那么通过图乙面积的计算，验证了一个恒等式，此等式是（ ）
A、a2﹣b2=（a+b）（a﹣b） B、（a﹣b）（a+2b）=a2+ab﹣b2 C、（a﹣b）2=a2﹣2ab+b2 D、（a+b）2=a2+2ab+b26. 如图，∠B=∠D=90°，CB=CD，∠1=30°，则∠2=（ ）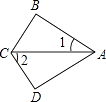
A、30° B、40° C、50° D、60°7. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
A、CB=CD B、∠BCA=∠DCA C、∠BAC=∠DAC D、∠B=∠D=90°8. 如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带（ ）去配.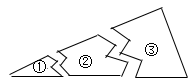
A、① B、② C、③ D、①和②二、填空题
-
9. 计算：（x+3）2= ．10. 计算：22018×0.52018= ．11. 命题“两直线平行，同位角相等”的逆命题是命题．（填“真”或“假”）12. 如图，已知△EFG≌△NMH，若EF=2.1，则MN= ．
13. （4a2﹣8a）÷2a= ．14. 若3m=6，9n=2，则3m﹣2n= ．15. 如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，点D在线段BE上.若∠1＝25°，∠2＝30°，则∠3＝.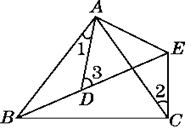
三、解答题
-
16. 先化简，再求值：a（1﹣4a）+（2a+1）（2a﹣1），其中a=4．17. 已知：如图，B、E、F、C四点在同一条直线上，AB=DC，BE=CF，∠B=∠ C．求证：△ABF≌△DCE．
18. 把下列各式分解因式：(1)、2x2﹣8x；(2)、6ab3﹣24a3b.19. 已知x+y=5，xy=1．(1)、求x2+y2的值．(2)、求（x﹣y）2的值．20. 如图，A，B两个建筑物分别位于河的两岸，要测得它们之间的距离，可以从B出发，沿河岸画一条射线BF，在BF上截取BC=CD，过D作DE∥AB，使A，C，E位于同一直线上，则DE的长就是A，B之间的距离．请你说明其中道理．
21. 如图所示，有两个长度相等的滑梯，左边滑梯BC的高AC与右边滑梯EF水平方向的长度DF相等，两滑梯倾斜角∠ABC和∠DFE有什么关系？
22. 某学校的操场是一个长方形，长为2x米，宽比长少5米，实施“阳光体育”行动以后，学校为了扩大学生的活动场地，让学生能更好地进行体育活动，将操场的长和宽都增加4米．(1)、求操场原来的面积是多少平方米（用代数式表示）？(2)、若x=20，求操场面积增加后比原来多多少平方米？23. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E，
(1)、当直线MN绕点C旋转到图（1）的位置时，显然有：DE=AD+BE；(2)、当直线MN绕点C旋转到图（2）的位置时，求证：DE=AD﹣BE；(3)、当直线MN绕点C旋转到图（3）的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写出这个等量关系．