吉林省白城市五校2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-08-15 类型：期中考试
一、单选题
-
1. 下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽，其中为中心对称图形的是（ ）．
A.
B.
C.
D.
A、A B、B C、C D、D2. 过多边形的一个顶点可以作7条对角线，则此多边形的内角和是外角和的（ ）A、4倍 B、5倍 C、6倍 D、3倍3. 一个三角形的两边长为3和8，第三边长为奇数，则第三边长为（ ）A、5或7 B、7或9 C、7 D、94. 若等腰三角形一腰上的高是腰长的一半，则这个等腰三角形的底角是（ ）A、75°或15° B、75° C、15° D、75°或30°5. 如图，△ABE≌△ACD，AB=AC，BE=CD，∠B=50°，∠AEC=120°，则∠DAC的度数等于（ ）
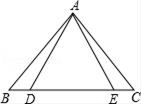A、120° B、70° C、60° D、50°6. 如图所示△ABC中，AB=AC，∠B=30°，AB⊥AD，AD=4cm，则BC的长为（ ）
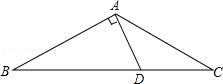A、8cm B、c4m C、12cm D、6cm二、填空题
-
7. 若一扇窗户打开后，用窗钩将其固定，主要运用的几何原理是。8. 如图，∠1=∠2，如果添加一个条件，即可得到△ABE≌△ACE，那么这个条件可以是（要求：不添加其他辅助线，写出一个条件即可）
9. 如图，∠1+∠2+∠3+∠4+∠5+∠6+∠7＝ ．
10. 小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图所示，则电子表的实际时刻是.
11. 点A（4，﹣2）关于y轴的对称点A′的坐标为.12. 已知4×2a×2a+1＝29 ， 且2a+b＝8，求ab＝ ．13. 如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AC于点E，垂足为点D，连接BE，则∠EBC的度数为 ．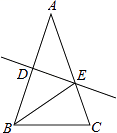
14. 如图，△ABC是等边三角形，D为AB的中点，DE⊥AC垂足为点E，EF∥AB，AE=1，则△EFC的周长=.
三、解答题
-
15. 先化简，再求值：2x2y•（﹣2xy2）3+（2xy）3•（﹣xy2）2 ， 其中x=4，y= ．16. 如图，已知AB∥DE ， AB＝DE ， BE＝CF ， 求证：AC∥DF ．
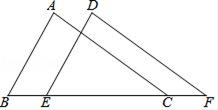17. 如图所示，在△ABC中，∠ABC和∠ACB的平分线交于点O，过O点作EF∥BC，交AB于E，交AC于F，若BE=3，CF=2，试求EF的值．
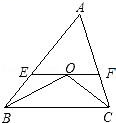18. 如图，在△ABC中，按以下步骤作图：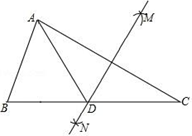
①分别以点A、C为圆心，以大于 AC的长为半径画弧，两弧相交于M、N两点；
②作直线MN交BC于点D，连接AD，若∠C=28°，AB=BD；
求∠B的度数．
19. 如图，已知△ABC和△BED都是等边三角形，且A、E、D在一条直线上，且DC=4，BD=2，求AD的长度？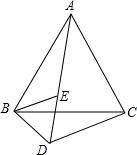
20. 如图，在5×5的正方形网格中，每个小正方形的边长均为1，线段AB的端点在格点上，按要求画出格点三角形，并求其面积．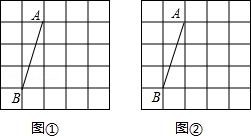
(1)、在图①中画出一个以AB为腰的等腰三角形ABC，其面积为.
(2)、在图②中画出一个以AB为底的等腰三角形ABC，其面积为.21. 如图∠BAC=30°，D为角平分线上一点，DE⊥AC于E，DF∥AC且交AB于F．
(1)、求证：△ADF是等腰三角形．(2)、若DF=10cm，求DE的长．22. 如图所示，若MP和NQ分别垂直平分AB和AC．
(1)、若△APQ的周长为12，求BC的长；(2)、∠BAC=105°，求∠PAQ的度数．23. 如图，在平面直角坐标系中，A（1，2），B（3，1），C（﹣2，﹣1）．
(1)、在图中作出△ABC关于y轴对称的△A1B1C1 ．(2)、△A1B1C1的面积为 ．(3)、在x轴上找出一点P，使PA+PB的值最小直接画出点P的位置．24. 如图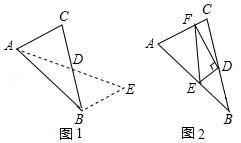
(1)、阅读理解：如图1，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE=AD，连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是.
(2)、问题解决：如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．25. 已知，△ABC是等腰直角三角形，BC=AB，A点在x负半轴上，直角顶点B在y轴上，点C在x轴上方．
(1)、如图1所示，若A的坐标是（﹣3，0），点B的坐标是（0，1），求点C的坐标；(2)、如图2，过点C作CD⊥y轴于D，请直接写出线段OA，OD，CD之间等量关系；(3)、如图3，若x轴恰好平分∠BAC，BC与x轴交于点E，过点C作CF⊥x轴于F，问CF与AE有怎样的数量关系？并说明理由．26. 如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．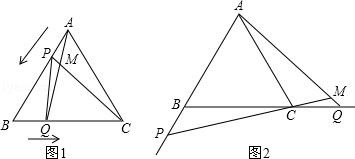
(1)、求证：△ABQ≌△CAP；(2)、当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．(3)、如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．