广东省肇庆市2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-08-15 类型：期中考试
一、单选题
-
1. 以下列各组线段的长为边，能组成三角形的是（ ）A、1cm、2cm、3cm B、1dm、5cm、6cm C、1dm、3cm、3cm D、2cm、4cm、7cm2. 下面有4个汽车标志图案，其中是轴对称图形的是（ ）
A、②③④ B、①②③ C、①②④ D、①③④3. 已知点A（x，4）与点B（3，y）关于y轴对称，那么x+y的值是（ ）A、﹣1 B、﹣7 C、7 D、14. 如图，在△ABC中，AB＝AC＝8，D是BC上一动点(D与B、C不重合)，且DE∥AB ， DF∥AC ， 则四边形DEAF的周长是（ ）
A、24 B、18 C、16 D、125. 如图，AC⊥BD于点P，AP=CP，增加下列一个条件：①BP=DP；②AB=CD；③∠A=∠C．其中能判定△ABP≌△CDP的条件有 （ ）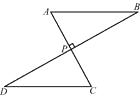
A、0个 B、1个 C、2个 D、3个6. 如图，在△ABC中，AD是角平分线，DE⊥AB于点E，△ABC的面积为7，AB=4，DE=2，则AC的长是（ ）
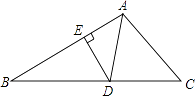A、4 B、3 C、6 D、57. 如图，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则三个结论：①AS=AR，②QP∥AR，③△BPR≌△QPS中一定正确的是（ ）
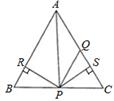A、全部正确 B、仅①和②正确 C、仅①正确 D、仅①和③正确8. 一个等腰三角形的一边长为4cm，另一边长为8cm，则该等腰三角形的周长是（ ）A、16cm B、20cm C、16cm或20cm D、不能确定9. 如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面的结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 如果一个十二边形的每个内角都是相等的，那么这个内角的度数是。11. 三角形的三边长分别为5，x，8，则x的取值范围是 ．12. 如图，已知OC平分∠AOB ， CD∥OB ， 若OD＝6cm，则CD的长为cm.
13.如图，在生活中，我们经常会看见在电线杆上拉两条钢线，来加固电线杆，这是利用了三角形的 ．
14. 如图，AB＝AC＝10，AB的垂直平分线DE交AB于点D，交AC于点E，则边BC的长度的取值范围是 ．
15. 如图，四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为 ．
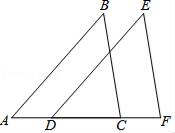
16. 完成下列证明过程．如图，已知AB∥DE，AB＝DE，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．
证明：∵AB∥DE
∴∠＝∠（）
∵AD＝CF
∴AD+DC＝CF+DC即
在△ABC和△DEF中AB＝DE
∴△ABC≌△DEF ．
三、解答题
-
17. 已知：如图，AB∥DE，AB＝DE，AC＝DF．求证：△ABF≌△DEC．
18. 如图，在Rt△ABC中，∠ACB=90°
(1)、用尺规作AB的垂直平分线MN交BC于点P（不写作法，保留作图痕迹）．(2)、连接AP，如果AP平分∠CAB，求∠B的度数．19. 如图，在平面直角坐标中，△ABC各顶点都在小方格的顶点上．
(1)、画出△ABC关于x轴对称的图形△A1B1C1；(2)、在y轴上找一点P，使PA+PB1最短，画出图形并写出P点的坐标．20. 如图，AB=AC，AC的垂直平分线MN交AB于D，交AC于E．
(1)、若∠A=40°，求∠BCD的度数；(2)、若AE=5，△BCD的周长17，求△ABC的周长．21. 如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE＝CD，DM⊥BC，垂足为M．
(1)、求∠E的度数．(2)、求证：M是BE的中点．22. 如图，△ABC中，∠ACB＝90°，以AC为边在△ABC外作等边三角形ACD，过点D作AC的垂线，垂足为F，与AB相交于点E，连接CE．
(1)、说明：AE＝CE＝BE；(2)、若AB＝15cm，P是直线DE上的一点．则当P在何处时，PB+PC最小，并求出此时PB+PC的值．23. 如图，△ABC和△AOD是等腰直角三角形，AB=AC ， AO=AD ， ∠BAC=∠OAD=90°，点O是△ABC内的一点，∠BOC=130°．
(1)、求证：OB=DC；(2)、求∠DCO的大小；(3)、设∠AOB=α ， 那么当α为多少度时，△COD是等腰三角形．24. 如图，△ABC是边长为4cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的是速度都为1厘米/秒．当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（秒）．
(1)、当运动时间为t秒时，AP的长为厘米，QC的长为厘米；（用含t的式子表示）(2)、当t为何值时，△PBQ是直角三角形？(3)、连接AQ、CP，相交于点M，如图2，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．