广东省肇庆市2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-08-15 类型:期中考试
一、单选题
-
1. 关于x的一元二次方程9x2-6x+k=0有两个不相等的实根,则k的范围是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 抛物线y=x2先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A、y=(x+1)2+3 B、y=(x+1)2﹣3 C、y=(x﹣1)2﹣3 D、y=(x﹣1)2+34. m是方程x2+x﹣1=0的根,则式子2m2+2m+2016的值为( )A、2013 B、2016 C、2017 D、20185. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ).
3. 抛物线y=x2先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A、y=(x+1)2+3 B、y=(x+1)2﹣3 C、y=(x﹣1)2﹣3 D、y=(x﹣1)2+34. m是方程x2+x﹣1=0的根,则式子2m2+2m+2016的值为( )A、2013 B、2016 C、2017 D、20185. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ). A、25° B、30° C、35° D、40°6. 2018年某县政府投资2亿元人民币建设了廉租房8万平方米,预计到2020年共投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年县政府投资的增长率为x,根据题意,列出方程为( )A、(81+x)2=9.5 B、2(1+x)2=9.5 C、2(1+x)2=8 D、2+2(1+x)+2(1+x)2=9.57. 已知点P(3a﹣9,1﹣a)是第三象限的点,且横坐标、纵坐标均为整数,若P、Q关于原点对称,点Q的坐标为( )A、(﹣3,﹣1) B、(3,1) C、(1,3) D、(﹣1,﹣3)8. 如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0,②2a﹣b=0,③a+b+c<0;④c﹣a=3,其中正确的有( )个.
A、25° B、30° C、35° D、40°6. 2018年某县政府投资2亿元人民币建设了廉租房8万平方米,预计到2020年共投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年县政府投资的增长率为x,根据题意,列出方程为( )A、(81+x)2=9.5 B、2(1+x)2=9.5 C、2(1+x)2=8 D、2+2(1+x)+2(1+x)2=9.57. 已知点P(3a﹣9,1﹣a)是第三象限的点,且横坐标、纵坐标均为整数,若P、Q关于原点对称,点Q的坐标为( )A、(﹣3,﹣1) B、(3,1) C、(1,3) D、(﹣1,﹣3)8. 如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0,②2a﹣b=0,③a+b+c<0;④c﹣a=3,其中正确的有( )个.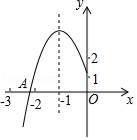 A、1 B、2 C、3 D、49. 如图,在边长为 的正方形 中,把边 绕点 逆时针旋转 ,得到线段 .连接 并延长交 于点 ,连接 ,则 的面积为( )
A、1 B、2 C、3 D、49. 如图,在边长为 的正方形 中,把边 绕点 逆时针旋转 ,得到线段 .连接 并延长交 于点 ,连接 ,则 的面积为( )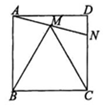 A、 B、 C、 D、10. 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A、 B、 C、 D、10. 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( ) A、
A、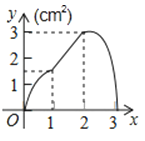 B、
B、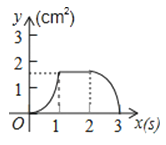 C、
C、 D、
D、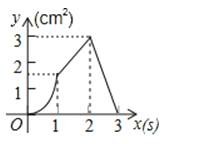
二、填空题
-
11. 将一个正六边形绕着其中心,至少旋转度可以和原来的图形重合.12. 已知x1 , x2是方程x2﹣3x﹣3=0的两根,不解方程可求得x12+x22= .13. 如图,将 绕点A逆时针旋转 ,得到 ,这时点 恰好在同一直线上,则 的度数为 .
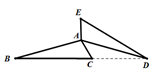 14. 若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为 .15. 如图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是 .
14. 若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为 .15. 如图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是 .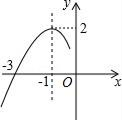 16. 如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
16. 如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
三、解答题
-
17. 解方程:x2﹣2x﹣3=0;18. 已知抛物线y=ax2+bx+c经过点A(1,0),B(﹣1,0),C(0,﹣2).求此抛物线的函数解析式和顶点坐标.19. 如图,在 中, , .
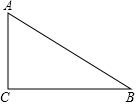 (1)、用直尺和圆规作 ,使圆心O在BC边,且 经过A,B两点上 不写作法,保留作图痕迹 ;(2)、连接AO,求证:AO平分 .20. 已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)、用直尺和圆规作 ,使圆心O在BC边,且 经过A,B两点上 不写作法,保留作图痕迹 ;(2)、连接AO,求证:AO平分 .20. 已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.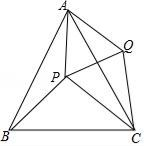 (1)、求证:PB=QC;(2)、若PA=3,PB=4,∠APB=150°,求PC的长度.21. 某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.(1)、试求y与x之间的函数关系式;(2)、当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?22. 将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图①的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.
(1)、求证:PB=QC;(2)、若PA=3,PB=4,∠APB=150°,求PC的长度.21. 某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.(1)、试求y与x之间的函数关系式;(2)、当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?22. 将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图①的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.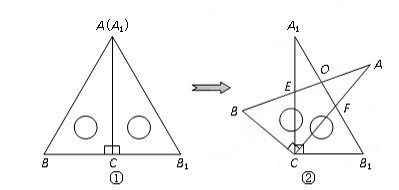 (1)、求证:△BCE≌△B1CF.(2)、当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.23. 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙,墙长25m,另外三边用木栏围着,木栏长40m.
(1)、求证:△BCE≌△B1CF.(2)、当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.23. 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙,墙长25m,另外三边用木栏围着,木栏长40m.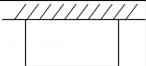 (1)、若养鸡场面积为200m2 , 求鸡场平行于墙的一边长.(2)、养鸡场面积能达到250m2吗?如果能,请给出设计方案,如果不能,请说明理由.24. 如图,在等边△ABC中,点D是AC边上一点,连接BD,过点A作AE⊥BD于E.
(1)、若养鸡场面积为200m2 , 求鸡场平行于墙的一边长.(2)、养鸡场面积能达到250m2吗?如果能,请给出设计方案,如果不能,请说明理由.24. 如图,在等边△ABC中,点D是AC边上一点,连接BD,过点A作AE⊥BD于E.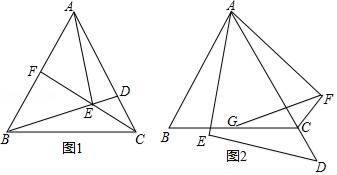 (1)、如图1,连接CE并延长CE交AB于点F,若∠CBD=15°,AB=4,求CE的长;(2)、如图2,当点D在线段AC的延长线上时,将线段AE绕点A逆时针旋转60°得到线段AF,连接EF,交BC于G,连接CF,求证:BG=CG.25. 如图,直线l:y=﹣ x+1与x轴、y轴分别交于点B、C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A.
(1)、如图1,连接CE并延长CE交AB于点F,若∠CBD=15°,AB=4,求CE的长;(2)、如图2,当点D在线段AC的延长线上时,将线段AE绕点A逆时针旋转60°得到线段AF,连接EF,交BC于G,连接CF,求证:BG=CG.25. 如图,直线l:y=﹣ x+1与x轴、y轴分别交于点B、C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A.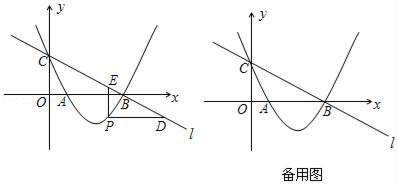 (1)、求该抛物线的解析式;(2)、若点P在直线l下方的抛物线上,过点P作PD∥x轴交l于点D,PE∥y轴交l于点E,求PD+PE的最大值;(3)、设F为直线l上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
(1)、求该抛物线的解析式;(2)、若点P在直线l下方的抛物线上,过点P作PD∥x轴交l于点D,PE∥y轴交l于点E,求PD+PE的最大值;(3)、设F为直线l上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.