广东省揭阳市惠来县2018-2019学年九年级上学期数学期中考试试卷

试卷更新日期：2019-08-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（）

A、x²﹣5x＝0 B、x+1＝0 C、y﹣2x＝0 D、2x³﹣2＝0

查看试题解析
2. 菱形不具备的性质是（）

A、四条边都相等 B、对角线一定相等 C、是轴对称图形 D、是中心对称图形

查看试题解析
3. 把 $ad = bc$ 写成比例式 $($ 其中a，b，c，d均不为 $0)$ ，下列选项中错误的是 $($ $)$

A、 $\frac{a}{b} = \frac{c}{d}$ B、 $\frac{b}{a} = \frac{d}{c}$ C、 $\frac{a}{c} = \frac{b}{d}$ D、 $\frac{c}{b} = \frac{a}{d}$

查看试题解析
4. 小亮是一名职业足球队员，根据以往比赛数据统计，小亮进球率为 $10 %$ ，他明天将参加一场比赛，下面几种说法正确的是（）

A、小亮明天的进球率为 $10 %$ B、小亮明天每射球10次必进球1次 C、小亮明天有可能进球 D、小亮明天肯定进球

查看试题解析
5. 如图，在 $Rt △ ABC$ 中， $∠ BAC = 90^{\circ}$ ， $AB = 3$ ， $AC = 4$ ，D为BC的中点，则线段AD的长为 $($ $)$

A、 $1.5$ B、2 C、 $2.5$ D、3

查看试题解析
6. 用配方法解一元二次方程x²﹣6x+1＝0，则配方后所得的方程为（）

A、（x+3）²＝10 B、（x+3）²＝8 C、（x﹣3）²＝10 D、（x﹣3）²＝8

查看试题解析
7. 已知线段a，b，c，d是比例线段，其中 $b = 2 cm$ ， $c = 3 cm$ ， $d = 6 cm$ ，则a等于 $($ $)$

A、1cm B、4cm C、9cm D、36cm

查看试题解析
8. 如图，矩形ABCD的两条对角线相交于点O，CE垂直平分DO， $AB = 1$ ，则BE等于 $($ $)$

A、 $\frac{3}{2}$ B、 $\frac{4}{3}$ C、 $\frac{2}{3}$ D、2

查看试题解析
9. 微信红包是沟通人们之间感情的一种方式，已知小明在2016年”元旦节”收到微信红包为300元，2018年为363元，若这两年小明收到的微信红包的年平均增长率为x，根据题意可列方程为（）

A、363（1+2x）=300 B、300（1+x²）=363 C、300（1+x）²=363 D、300+x²=363

查看试题解析
10. 如图，在边长为2的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连接PB、PQ，则 $△ PBQ$ 周长的最小值为 $($ $)$

A、 $\sqrt{5}$ B、3 C、 $\sqrt{5} + 1$ D、 $2 \sqrt{2}$

查看试题解析

二、填空题

11. 一元二次方程 ${(x + 1)}^{2} = 16$ 的解是．

查看试题解析
12. 把一元二次方程3x（x﹣2）=4化为一般形式是．

查看试题解析
13. 若 $\frac{a}{b} = \frac{2}{9}$ ，则 $\frac{a + b}{b} =$ .

查看试题解析
14. 为了估计鱼塘里有多少条鱼，先从鱼塘中打捞 $60$ 条鱼，把每条鱼都做上标记，放回鱼塘，几天后，又从鱼塘中打捞上 $50$ 条鱼，结果 $2$ 条鱼有标记，那么这个鱼塘里大约有鱼条．

查看试题解析
15. 关于 $x$ 的方程 $m x^{2} - 2 x + 3 = 0$ 有两个不相等的实数根，那么 $m$ 的取值范围是．

查看试题解析
16. 如图，正方形ABCD中， $AB = 6$ ，点E在边CD上，且 $CD = 3 DE$ ，将 $△ ADE$ 沿AE对折至 $△ AFE .$ 延长EF交边BC于点G，连接AG、 $CF .$ 下列结论： $① △ ABG$ ≌ $△ AFG$ ； $② BG = GC$ ； $③ AG / / CF$ ； $④ △ GCF$ 是等边三角形，其中正确结论有．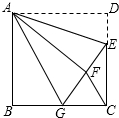

查看试题解析

三、解答题

17. 已知3是一元二次方程x²-2x+a=0的一个根，求a的值和方程的另一个根.

查看试题解析
18. 解方程：x²－2x－4＝0．

查看试题解析
19. 如图，直线 $l_{1} / / l_{2} / / l_{3}$ ，直线AC依次交 $l_{1}$ 、 $l_{2}$ 、 $l_{3}$ 于A、B、C三点，直线DF依次交 $l_{1}$ 、 $l_{2}$ 、 $l_{3}$ 于D、E、F三点，若 $\frac{AB}{AC} = \frac{4}{7}$ ， $DE = 2$ ，求EF的长．

查看试题解析
20. 如图，BD为平行四边形ABCD的对角线，按要求完成下列各题．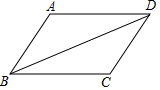

(1)、用直尺和圆规作出对角线BD的垂直平分线交AD于点E，交BC于点F，垂足为O，连接BE和DF， $($ 保留作图痕迹；不要求写作法 $)$

(2)、在 $(1)$ 的基础上，求证： $E O = F O$ ．

查看试题解析
21. 如图，某小区规划在长32米，宽20米的矩形场地ABCD上修建三条同样宽的3条小路，使其中两条与AB平行，一条与AD平行，其余部分种植草坪，若使草坪的面积为570米 $^{2}$ ，问小路宽为多少米？

查看试题解析
22. 如图所示，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F，且AF＝BD，连接BF.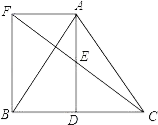

(1)、求证：D是BC的中点；

(2)、若AB＝AC，试判断四边形AFBD的形状，并证明你的结论.

查看试题解析
23. 为了解全校学生上学的交通方式，该校九年级 $(8)$ 班的4名同学联合设计了一份调查问卷，对该校部分学生进行了随机调查 $.$ 按 $A ($ 骑自行车 $)$ 、 $B ($ 乘公交车 $)$ 、 $C ($ 步行 $)$ 、 $D ($ 乘私家车 $)$ 、 $E ($ 其他方式 $)$ 设置选项，要求被调查同学从中单选，并将调查结果绘制成条形统计图1和扇形统计图2，根据以上信息，解答下列问题：

(1)、本次接受调查的总人数是人，并把条形统计图补充完整；

(2)、在扇形统计图中，“乘私家车的人数所占的百分比是， “其他方式”所在扇形的圆心角度数是度；

(3)、已知这4名同学中有2名女同学，要从中选两名同学汇报调查结果，请你用列表法或画树状图的方法，求出恰好选出1名男生和1名女生的概率．

查看试题解析
24. 中秋节前夕，某公司的李会计受公司委派去超市购买若干盒美心月饼，超市给出了该种月饼不同购买数量的价格优惠，如图，折线ABCD表示购买这种月饼每盒的价格y（元）与盒数x（盒）之间的函数关系．

(1)、当购买这种月饼盒数不超过10盒时，一盒月饼的价格为元；

(2)、求出当10＜x＜25时，y与x之间的函数关系式；

(3)、当时李会计支付了3600元购买这种月饼，那么李会计买了多少盒这种月饼？

查看试题解析
25.
如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．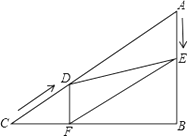

(1)、求证：AE=DF；

(2)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；

(3)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析