广东省广州市花都区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-08-15 类型:期中考试
一、单选题
-
1. 如图图形中,既是轴对称图形,又是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 平面直角坐标系内一点 关于原点对称的点的坐标是A、 B、 C、 D、3. 抛物线 经过平移得到 ,平移方法是A、向左平移1个单位,再向下平移3个单位 B、向左平移1个单位,再向上平移3个单位 C、向右平移1个单位,再向下平移3个单位 D、向右平移1个单位,再向上平移3个单位4. 下列一元二次方程中没有实数根是A、 B、 C、 D、5. 一元二次方程x2+6x﹣5=0配方后变形正确的是( )A、(x﹣3)2=14 B、(x+3)2=4 C、(x+6)2= D、(x+3)2=146. 如图,将 绕点A按逆时针方向旋转 ,得到 ,若点 在线段BC的延长线上,则 的大小为
2. 平面直角坐标系内一点 关于原点对称的点的坐标是A、 B、 C、 D、3. 抛物线 经过平移得到 ,平移方法是A、向左平移1个单位,再向下平移3个单位 B、向左平移1个单位,再向上平移3个单位 C、向右平移1个单位,再向下平移3个单位 D、向右平移1个单位,再向上平移3个单位4. 下列一元二次方程中没有实数根是A、 B、 C、 D、5. 一元二次方程x2+6x﹣5=0配方后变形正确的是( )A、(x﹣3)2=14 B、(x+3)2=4 C、(x+6)2= D、(x+3)2=146. 如图,将 绕点A按逆时针方向旋转 ,得到 ,若点 在线段BC的延长线上,则 的大小为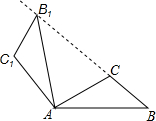 A、 B、 C、 D、7. 若x支球队参加篮球比赛,共比赛了36场,每2队之间比赛一场,则下列方程中正确的是A、 B、 C、 D、8. 在同一直角坐标系中 与 图象大致为A、
A、 B、 C、 D、7. 若x支球队参加篮球比赛,共比赛了36场,每2队之间比赛一场,则下列方程中正确的是A、 B、 C、 D、8. 在同一直角坐标系中 与 图象大致为A、 B、
B、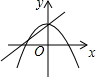 C、
C、 D、
D、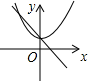 9. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
9. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( ) A、(4n﹣1, ) B、(2n﹣1, ) C、(4n+1, ) D、(2n+1, )
A、(4n﹣1, ) B、(2n﹣1, ) C、(4n+1, ) D、(2n+1, )二、填空题
-
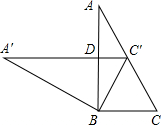
10. 已知 是关于x的一元二次方程,则 .11. 若 , 是方程 的两根,则 .12. 如图,两块相同的三角板完全重合在一起, , ,把上面一块绕直角顶点B逆时针旋转到 的位置,点 在AC上, 与AB相交于点D,则 .
 13. 抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .
13. 抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .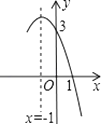 14. 二次函数 图象如图,下列结论: ; ; ; 当 时, : .
14. 二次函数 图象如图,下列结论: ; ; ; 当 时, : .其中正确的有 只填序号 .
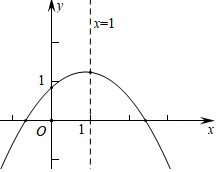
三、解答题
-
15. 已知 、 是抛物线 上的两点,则 填 、 、 .16. 解方程:(1)、(2)、17. 已知:如图,在 中, ,将 绕点B按逆时针方向旋转 得到 ,点C在边BD上.
求: 的度数.
 18. 如图,在边长为1个单位长度的正方形网格中建立平面直角坐标系, 的顶点都在格点上,请解答下列问题: 不需要作图过程
18. 如图,在边长为1个单位长度的正方形网格中建立平面直角坐标系, 的顶点都在格点上,请解答下列问题: 不需要作图过程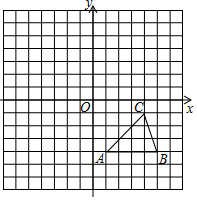 (1)、画出以点A为旋转中心, 沿逆时针方向旋转 后的图形 ;(2)、以原点O为对称中心,画出 关于点O的中心对称图形 ;(3)、若在x轴上存在点P,使得 最小,则点P的坐标为 .19. 某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,求这种药品下降的百分率.20. 已知抛物线
(1)、画出以点A为旋转中心, 沿逆时针方向旋转 后的图形 ;(2)、以原点O为对称中心,画出 关于点O的中心对称图形 ;(3)、若在x轴上存在点P,使得 最小,则点P的坐标为 .19. 某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,求这种药品下降的百分率.20. 已知抛物线 (1)、对称轴为 , 顶点坐标为;(2)、在坐标系中利用五点法画出此抛物线.
(1)、对称轴为 , 顶点坐标为;(2)、在坐标系中利用五点法画出此抛物线. (3)、若抛物线与x轴交点为A、B,点 在抛物线上,求 的面积.21. 已知:关于x的方程 .(1)、若方程总有两个实数根,求m的取值范围;(2)、在(1)的条件下,若两实数根 、 满足 ,求m的值.22. 为满足市场需求,某超市在八月十五“中秋节”来临前夕,购进一种品牌的月饼,每盒进价40元,根据以往的销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.(1)、写出每天的销售量 盒 与每盒月饼上涨 元 之间的函数关系式.(2)、当每盒售价定为多少元时,当天的销售利润 元 最大?最大利润是多少?(3)、为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的 ,那么超市每天获得最大利润是多少?23. 已知:如图,抛物线 与x轴交于A、B两点,与y轴交于C点,且 、 ,点D是第四象限的抛物线上的一个动点,过点D作直线 轴,垂足为点F,交线段BC于点E
(3)、若抛物线与x轴交点为A、B,点 在抛物线上,求 的面积.21. 已知:关于x的方程 .(1)、若方程总有两个实数根,求m的取值范围;(2)、在(1)的条件下,若两实数根 、 满足 ,求m的值.22. 为满足市场需求,某超市在八月十五“中秋节”来临前夕,购进一种品牌的月饼,每盒进价40元,根据以往的销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.(1)、写出每天的销售量 盒 与每盒月饼上涨 元 之间的函数关系式.(2)、当每盒售价定为多少元时,当天的销售利润 元 最大?最大利润是多少?(3)、为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的 ,那么超市每天获得最大利润是多少?23. 已知:如图,抛物线 与x轴交于A、B两点,与y轴交于C点,且 、 ,点D是第四象限的抛物线上的一个动点,过点D作直线 轴,垂足为点F,交线段BC于点E (1)、求抛物线的解析式及点A的坐标;(2)、当 时,求点D的坐标;(3)、在y轴上是否存在P点,使得 是以AC为腰的等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.24. 如图1,在 中,点D、E分别在AB、AC上, , ,
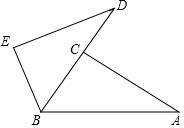
(1)、求抛物线的解析式及点A的坐标;(2)、当 时,求点D的坐标;(3)、在y轴上是否存在P点,使得 是以AC为腰的等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.24. 如图1,在 中,点D、E分别在AB、AC上, , , (1)、求证: ;(2)、若 ,把 绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
(1)、求证: ;(2)、若 ,把 绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.判断 的形状,并说明理由;
把 绕点A在平面内自由旋转,若 , ,试问 面积是否存在最大值;若存在,求出其最大值 若不存在,请说明理由.