2017年浙江省台州市中考数学试卷
试卷更新日期:2017-06-21 类型:中考真卷
一、选择题
-
1. 5的相反数是( )
A、 5 B、 C、 D、2.如图所示的工件是由两个长方体构成的组合体,则它的主视图是( )
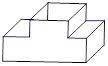 A、
A、 B、
B、 C、
C、 D、
D、 3. 人教版初中数学教科书共6册,总字数是978000,用科学记数法可将978000表示为( )A、 B、 C、 D、4. 有5名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的( )
3. 人教版初中数学教科书共6册,总字数是978000,用科学记数法可将978000表示为( )A、 B、 C、 D、4. 有5名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的( )
A、方差 B、中位数 C、众数 D、平均数5.如图,点P是∠AOB平分线上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA 的距离是( )
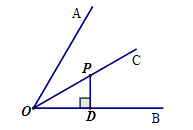 A、1 B、2 C、 D、46. 已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为 ,当电压为定值时,I关于R的函数图象是( )
A、1 B、2 C、 D、46. 已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为 ,当电压为定值时,I关于R的函数图象是( )
A、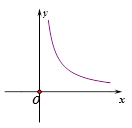 B、
B、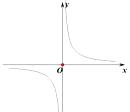 C、
C、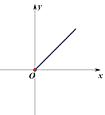 D、
D、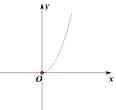 7. 下列计算正确的是( )
7. 下列计算正确的是( )
A、 B、 C、 D、8.如图,已知△ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
 A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE9. 滴滴快车是一种便捷的出行工具,计价规则如下表:
A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE9. 滴滴快车是一种便捷的出行工具,计价规则如下表:计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.3元/分钟
0.8元/公里
注:车费由里程费、时长费、远途费三部分,其中里程费按行车的实际里程计费;时长费按行车的实际时间计算,远途费的收取方式为:行车7公里以内(含7公里)不收远途费
超过7公里的,超出部分每公里收0.8元
小王与小张各自乘坐滴滴快车,行车里程分别为6公里和8.5公里,如果下车时所付车费相同,那么这两辆滴滴快车的行车时间相差( )
A、10分钟 B、13分钟 C、15分钟 D、19分钟10.如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 时,则 为( )
 A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题
-
11. 因式分解: .
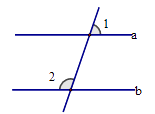
12.如图,已知直线a∥b,∠1=70°,则∠2=
 13.
13.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30cm,则
弧BC的长为cm(结果保留 )
 14. 商家花费760元购进某种水果80千克,销售中有5%的水果正常损耗,为了避免亏本,售价至少应定为元/千克
14. 商家花费760元购进某种水果80千克,销售中有5%的水果正常损耗,为了避免亏本,售价至少应定为元/千克
15. 三名运动员参加定点投篮比赛,原定出场顺序是:甲第一个出场,乙第二个出场,丙第三个出场,由于某种原因,要求这三名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为
16.如图,有一个不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是

三、解答题
-
17. 计算:
18. 先化简,再求值: ,其中
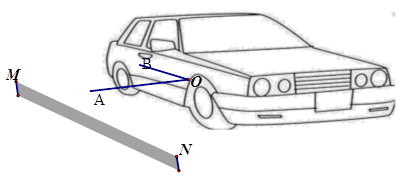
19.如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
 20.
20.如图,直线 : 与直线 : 相交于点P(1,b)
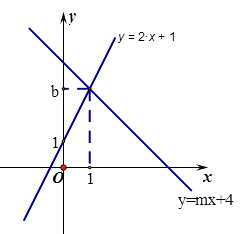 (1)、求b,m的值(2)、垂直于x轴的直线 与直线 , 分别相交于C,D,若线段CD长为2,求a的值21. 家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康。某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查
(1)、求b,m的值(2)、垂直于x轴的直线 与直线 , 分别相交于C,D,若线段CD长为2,求a的值21. 家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康。某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查
(1)、下列选取样本的方法最合理的一种是(只需填上正确答案的序号)①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取③在全市常住人口中以家庭为单位随机抽取.
(2)、本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下图:
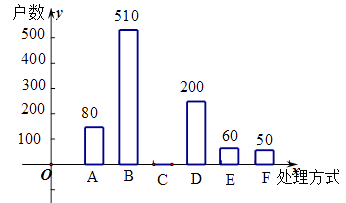

①求m、n的值.
②补全条形统计图
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点。
22.如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
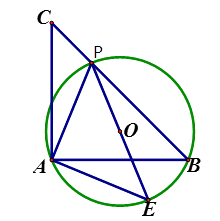 (1)、求证:△APE是等腰直角三角形;(2)、若⊙O的直径为2,求 的值23. 交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
(1)、求证:△APE是等腰直角三角形;(2)、若⊙O的直径为2,求 的值23. 交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)、根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ② ③(2)、请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?(3)、已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:①市交通运行监控平台显示,当 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值
24.在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程 ,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。
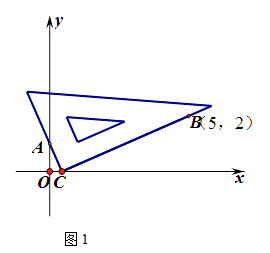
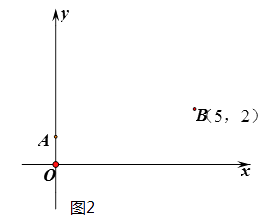 (1)、在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)(2)、结合图1,请证明“第三步”操作得到的m就是方程 的一个实数根;(3)、上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 的实数根,请你直接写出一对固定点的坐标;(4)、实际上,(3)中的固定点有无数对,一般地,当 , , , 与a,b,c之间满足怎样的关系时,点P( , ),Q( , )就是符合要求的一对固定点?
(1)、在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)(2)、结合图1,请证明“第三步”操作得到的m就是方程 的一个实数根;(3)、上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 的实数根,请你直接写出一对固定点的坐标;(4)、实际上,(3)中的固定点有无数对,一般地,当 , , , 与a,b,c之间满足怎样的关系时,点P( , ),Q( , )就是符合要求的一对固定点?