新疆生产建设兵团2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-14 类型:期末考试
一、单选题
-
1. 下列长度的三条线段,能组成三角形的是 ( )A、1,2,3 B、1,4,2 C、2,3,4 D、6,2,32. 医学研究发现某病毒直径约为 毫米,这个数用科学记数法表示为A、 B、 C、 D、3. 点P(1,2)关于y轴对称点的坐标是( )A、(﹣1,2) B、(1,﹣2) C、(1,2) D、(﹣1,﹣2)4. 下列运算中正确的是( )A、 B、 C、 D、5. 已知 是一个完全平方式,则k的值是A、12 B、 C、6 D、6. 小明通常上学时走上坡路,通常的速度为m千米/时,放学回家时,沿原路返回,通常的速度为n千米/时,则小明上学和放学路上的平均速度为( )千米/时A、 B、 C、 D、7. 如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
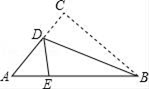 A、9cm B、13cm C、16cm D、10cm8. 如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带________去配.( )
A、9cm B、13cm C、16cm D、10cm8. 如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带________去配.( )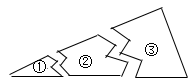 A、① B、② C、③ D、①和②
A、① B、② C、③ D、①和②二、填空题
-
9. 分式 有意义,则x的取值范围是.10. 如图,AB=AC,要使△ABE≌△ACD,应添加的条件是(添加一个条件即可)。
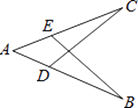 11. 如图,△ABC中,AB=AC,∠BAC=124°,AD是BC边上的中线,且BD=BE,则∠ADE是度.
11. 如图,△ABC中,AB=AC,∠BAC=124°,AD是BC边上的中线,且BD=BE,则∠ADE是度. 12. 已知a+ =2,求a2+ = .13. 若 ,则 的值为 .14. 分解因式: .15. 一个等腰三角形的两边长分别为2和5,则它的周长为。16. 如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若 , , , 的外角和等于 ,则 的度数为.
12. 已知a+ =2,求a2+ = .13. 若 ,则 的值为 .14. 分解因式: .15. 一个等腰三角形的两边长分别为2和5,则它的周长为。16. 如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若 , , , 的外角和等于 ,则 的度数为.
三、解答题
-
17. 计算(1)、(2)、(3)、(4)、18.(1)、运用多项式乘法,计算下列各题:
①(x+2)(x+3)=
②(x+2)(x﹣3)=
③(x﹣3)(x﹣1)=
(2)、若:(x+a)(x+b)=x2+px+q,根据你所发现的规律,直接填空:p= , q=.(用含a、b的代数式表示)19. 惠阳区某中学2016年在商场购买甲、乙两种不同的足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元(1)、求购买一个甲种足球,一个乙种足球各需多少元?(2)、2017年为响应习总书记“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,预算金额不超过3000元.去到商场时恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果该学校此次需购买20个乙种足球,请问该学校购买这批足球所用金额是否会超过预算?20. 如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你用直尺和圆规画出灯柱的位置点P.(不写作图步骤,保留作图痕迹)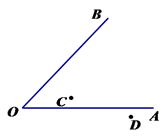 21. 先化简,再求值: ,其中x=2.22. 解方程:(1)、(2)、 .23. 如图,已知 中, , ,求证: .
21. 先化简,再求值: ,其中x=2.22. 解方程:(1)、(2)、 .23. 如图,已知 中, , ,求证: .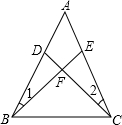 24. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
24. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.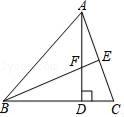 (1)、若∠BAC=60°,∠C=70°,求∠AFB的大小;(2)、若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.25. 如图
(1)、若∠BAC=60°,∠C=70°,求∠AFB的大小;(2)、若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.25. 如图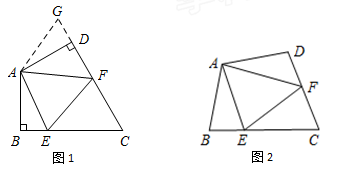 (1)、如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是 BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是什么;
(1)、如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是 BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是什么;探索延伸:
(2)、如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=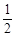 ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.