江苏省常州市2019年中考数学试卷
试卷更新日期:2019-08-14 类型:中考真卷
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 若代数式 有意义,则实数 的取值范围是( )A、 B、 C、 D、3. 如图是某几何体的三视图,该几何体是( )
 A、圆柱 B、正方体 C、圆锥 D、球4. 如图,在线段 、 、 、 中,长度最小的是( )
A、圆柱 B、正方体 C、圆锥 D、球4. 如图,在线段 、 、 、 中,长度最小的是( ) A、线段 B、线段 C、线段 D、线段5. 若 ,相似比为 ,则 与 的周长的比为( )A、 B、 C、 D、6. 下列各数中与 的积是有理数的是( )A、 B、 C、 D、7. 判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )A、﹣2 B、﹣ C、0 D、8. 随着时代的进步,人们对 (空气中直径小于等于 微米的颗粒)的关注日益密切.某市一天中 的值 ( )随时间 ( )的变化如图所示,设 表示 时到 时 的值的极差(即 时到 时 的最大值与最小值的差),则 与 的函数关系大致是( )
A、线段 B、线段 C、线段 D、线段5. 若 ,相似比为 ,则 与 的周长的比为( )A、 B、 C、 D、6. 下列各数中与 的积是有理数的是( )A、 B、 C、 D、7. 判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )A、﹣2 B、﹣ C、0 D、8. 随着时代的进步,人们对 (空气中直径小于等于 微米的颗粒)的关注日益密切.某市一天中 的值 ( )随时间 ( )的变化如图所示,设 表示 时到 时 的值的极差(即 时到 时 的最大值与最小值的差),则 与 的函数关系大致是( )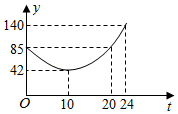 A、
A、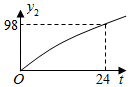 B、
B、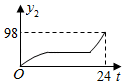 C、
C、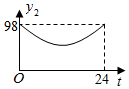 D、
D、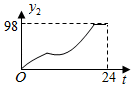
二、填空题
-
9. 计算: .10. 4的算术平方根是 , 9的平方根是 , ﹣27的立方根是 .11. 分解因式: .12. 如果∠α=35°,那么∠α的余角为.13. 如果 ,那么代数式 的值是.14. 平面直角坐标系中,点 到原点的距离是.15. 若 ,是关于 、 的二元一次方程 的解,则 .16. 如图, 是⊙ 的直径, 、 是⊙ 上的两点, ,则 .
 17. 如图,半径为 的⊙ 与边长为 的等边三角形 的两边 、 都相切,连接 ,则 .
17. 如图,半径为 的⊙ 与边长为 的等边三角形 的两边 、 都相切,连接 ,则 .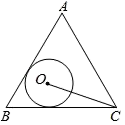 18. 如图,在矩形 中, ,点 是 的中点,点 在 上, ,点 、 在线段 上.若 是等腰三角形且底角与 相等,则 .
18. 如图,在矩形 中, ,点 是 的中点,点 在 上, ,点 、 在线段 上.若 是等腰三角形且底角与 相等,则 .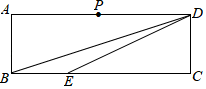
三、解答题
-
19. 计算:(1)、(2)、 .20. 解不等式组 并把解集在数轴上表示出来.21. 如图,把平行四边形纸片 沿 折叠,点 落在点 处, 与 相交于点 .
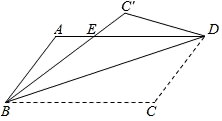 (1)、连接 ,则 与 的位置关系是;(2)、 与 相等吗?证明你的结论.22. 在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
(1)、连接 ,则 与 的位置关系是;(2)、 与 相等吗?证明你的结论.22. 在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图. (1)、本次调查的样本容量是 , 这组数据的众数为元;(2)、求这组数据的平均数;(3)、该校共有 学生参与捐款,请你估计该校学生的捐款总数.23. 将图中的 型(正方形)、 型(菱形)、 型(等腰直角三角形)纸片分别放在 个盒子中,盒子的形状、大小、质地都相同,再将这 个盒子装入一只不透明的袋子中.
(1)、本次调查的样本容量是 , 这组数据的众数为元;(2)、求这组数据的平均数;(3)、该校共有 学生参与捐款,请你估计该校学生的捐款总数.23. 将图中的 型(正方形)、 型(菱形)、 型(等腰直角三角形)纸片分别放在 个盒子中,盒子的形状、大小、质地都相同,再将这 个盒子装入一只不透明的袋子中. (1)、搅匀后从中摸出 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是;(2)、搅匀后先从中摸出 个盒子(不放回),再从余下的 个盒子中摸出 个盒子,把摸出的 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)24. 甲、乙两人每小时共做 个零件,甲做 个零件所用的时间与乙做 个零件所用的时间相等.甲、乙两人每小时各做多少个零件?25. 如图,在 中, , ,点 在 轴上,点 是 的中点,反比例函数 的图象经过点 、
(1)、搅匀后从中摸出 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是;(2)、搅匀后先从中摸出 个盒子(不放回),再从余下的 个盒子中摸出 个盒子,把摸出的 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)24. 甲、乙两人每小时共做 个零件,甲做 个零件所用的时间与乙做 个零件所用的时间相等.甲、乙两人每小时各做多少个零件?25. 如图,在 中, , ,点 在 轴上,点 是 的中点,反比例函数 的图象经过点 、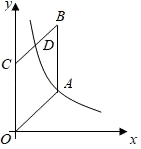 (1)、求 的值;(2)、求点 的坐标.26. 【阅读】数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.(1)、【理解】
(1)、求 的值;(2)、求点 的坐标.26. 【阅读】数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.(1)、【理解】如图,两个边长分别为 、 、 的直角三角形和一个两条直角边都是 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
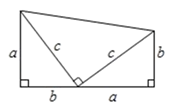 (2)、如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ;
(2)、如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ; (3)、【运用】
(3)、【运用】边形有 个顶点,在它的内部再画 个点,以( )个点为顶点,把 边形剪成若干个三角形,设最多可以剪得 个这样的三角形.当 , 时,如图,最多可以剪得 个这样的三角形,所以 .
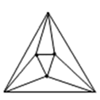
①当 , 时,如图, ;当 , 时, ;
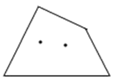
②对于一般的情形,在 边形内画 个点,通过归纳猜想,可得 (用含 、 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
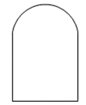
27. 已知平面图形 ,点 、 是 上任意两点,我们把线段 的长度的最大值称为平面图形 的“宽距”.例如,正方形的宽距等于它的对角线的长度.(1)、写出下列图形的宽距:①半径为 的圆:;
②如图,上方是半径为 的半圆,下方是正方形的三条边的“窗户形“:;
 (2)、如图,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .
(2)、如图,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .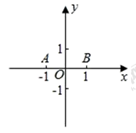
①若 ,用直尺和圆规画出点 所在的区域并求它的面积(所在区域用阴影表示);
②若点 在⊙ 上运动,⊙ 的半径为 ,圆心 在过点 且与 轴垂直的直线上.对于⊙ 上任意点 ,都有 ,直接写出圆心 的横坐标 的取值范围.