湖北省孝感市2019年中考数学试卷
试卷更新日期:2019-08-14 类型:中考真卷
一、单选题
-
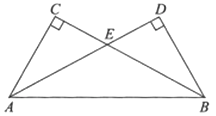
1. 计算 等于( )A、 B、 C、1 D、392. 如图,直线 ,直线 与 , 分别交于点 , , 交 于点 ,若 ,则 的度数为( )
 A、10° B、20° C、30° D、40°3. 下列立体图形在,左视图是圆的是( )A、
A、10° B、20° C、30° D、40°3. 下列立体图形在,左视图是圆的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列说法错误的是( )A、在一定条件下,可能发生也可能不发生的事件称为随机事件 B、一组数据中出现次数最多的数据称为这组数据的众数 C、方差可以刻画数据的波动程度,方差越大,波动越小;方差越小,波动越大 D、全面调查和抽样调查是收集数据的两种方式5. 下列计算正确的是( )A、 B、 C、 D、6. 公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬根撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力 (单位: )关于动力臂l(单位: )的函数解析式正确的是( )A、 B、 C、 D、7. 已知二元一次方程组 ,则 的值是( )A、 B、5 C、 D、68. 如图,在平面直角坐标系中,将点 绕原点 顺时针旋转90°得到点 ,则 的坐标为( )
4. 下列说法错误的是( )A、在一定条件下,可能发生也可能不发生的事件称为随机事件 B、一组数据中出现次数最多的数据称为这组数据的众数 C、方差可以刻画数据的波动程度,方差越大,波动越小;方差越小,波动越大 D、全面调查和抽样调查是收集数据的两种方式5. 下列计算正确的是( )A、 B、 C、 D、6. 公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬根撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力 (单位: )关于动力臂l(单位: )的函数解析式正确的是( )A、 B、 C、 D、7. 已知二元一次方程组 ,则 的值是( )A、 B、5 C、 D、68. 如图,在平面直角坐标系中,将点 绕原点 顺时针旋转90°得到点 ,则 的坐标为( )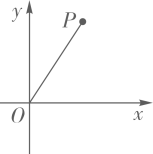 A、 B、 C、 D、9. 一个装有进水管和出水管的空容器,从某时刻开始 内只进水不出水,容器内存水 ,在随后的 内既进水又出水,容器内存水 ,接着关闭进水管直到容器内的水放完.若每分钟进水和出水量是两个常数,容器内的水量 (单位: )与时间 (单位: )之间的函数关系的图象大致的是( )A、
A、 B、 C、 D、9. 一个装有进水管和出水管的空容器,从某时刻开始 内只进水不出水,容器内存水 ,在随后的 内既进水又出水,容器内存水 ,接着关闭进水管直到容器内的水放完.若每分钟进水和出水量是两个常数,容器内的水量 (单位: )与时间 (单位: )之间的函数关系的图象大致的是( )A、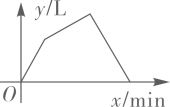 B、
B、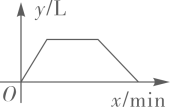 C、
C、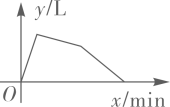 D、
D、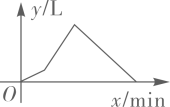 10. 如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为( )
10. 如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为( )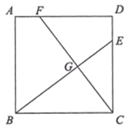 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
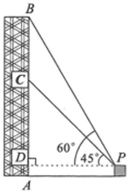
11. 中国“神威·太湖之光”计算机最高运行速度为1250000000亿次/秒,将数1250000000用科学记数法可表示为.12. 方程 的解为.13. 如图,在 处利用测角仪测得某建筑物 的顶端 点的仰角为60°,点 的仰角为45°,点 到建筑物的距离为 米,则 米.
 14. 董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,将他们绘制了两幅不完整的统计图( .小于5天; .5天; .6天; .7天),则扇形统计图 部分所对应的圆心角的度数是.
14. 董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,将他们绘制了两幅不完整的统计图( .小于5天; .5天; .6天; .7天),则扇形统计图 部分所对应的圆心角的度数是.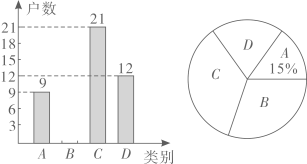 15. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图,若用圆的内接正十二边形的面积 来近似估计 的面积 ,设 的半径为1,则 .
15. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图,若用圆的内接正十二边形的面积 来近似估计 的面积 ,设 的半径为1,则 . 16. 如图,双曲线 经过矩形OABC的顶点 ,双曲线 交 , 于点 , ,且与矩形的对角线 交于点 ,连接 .若 ,则 的面积为.
16. 如图,双曲线 经过矩形OABC的顶点 ,双曲线 交 , 于点 , ,且与矩形的对角线 交于点 ,连接 .若 ,则 的面积为.
三、解答题
-
17. 计算: .18. 如图,已知 , 与 交于点 , ,求证: .
 19. 一个不透明的袋子中装有四个小球,上面分别标有数字-2,-1,0,1,它们除了数字不一样外,其它完全相同.
19. 一个不透明的袋子中装有四个小球,上面分别标有数字-2,-1,0,1,它们除了数字不一样外,其它完全相同.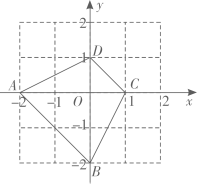 (1)、随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是.(2)、小聪先从袋子中随机摸出一个小球,记下数字作为点 的纵坐标,如图,已知四边形 的四个顶点的坐标分别为 , , , ,请用画树状图或列表法,求点 落在四边形 所围成的部分内(含边界)的概率.20. 如图, 中, ,一同学利用直尺和圆规完成如下操作:
(1)、随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是.(2)、小聪先从袋子中随机摸出一个小球,记下数字作为点 的纵坐标,如图,已知四边形 的四个顶点的坐标分别为 , , , ,请用画树状图或列表法,求点 落在四边形 所围成的部分内(含边界)的概率.20. 如图, 中, ,一同学利用直尺和圆规完成如下操作:①以点 为圆心,以 为半径画弧,角 于点 ;分别以点 、 为圆心,以大于 的长为半径画弧,两弧交点 ,作射线 ;
②以点 为圆心,以适当的长为半径画弧,交 于点 ,交 的延长线于点 ;分别以点 、 为圆心,以大于 的长为半径画弧,两弧交于点 ,作直线 交 的延长线于点 ,交射线 于点 .
请你观察图形,根据操作结果解答下列问题;
 (1)、线段 与 的大小关系是.(2)、过点 作 交 的延长线于点 ,若 , ,求 的值.21. 已知关于 的一元二次方程 有两个不相等的实数根 , .(1)、若 为正数,求 的值;(2)、若 , 满足 ,求 的值.22. 为了加快“智慧校园”建设,某市准备为试点学校采购一批 、 两种型号的一体机,经过市场调查发现,今年每套 型一体机的价格比每套 型一体机的价格多0.6万元,且用960万元恰好能购买500套 型一体机和200套 型一体机.(1)、求今年每套 型、 型一体机的价格各是多少万元(2)、该市明年计划采购 型、 型一体机1100套,考虑物价因素,预计明年每套 型一体机的价格比今年上涨25%,每套 型一体机的价格不变,若购买 型一体机的总费用不低于购买 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?23. 如图,点 是 的内心, 的延长线与 的外接圆 交于点 ,与 交于点 ,延长 、 相交于点 , 的平分线交 于点 .
(1)、线段 与 的大小关系是.(2)、过点 作 交 的延长线于点 ,若 , ,求 的值.21. 已知关于 的一元二次方程 有两个不相等的实数根 , .(1)、若 为正数,求 的值;(2)、若 , 满足 ,求 的值.22. 为了加快“智慧校园”建设,某市准备为试点学校采购一批 、 两种型号的一体机,经过市场调查发现,今年每套 型一体机的价格比每套 型一体机的价格多0.6万元,且用960万元恰好能购买500套 型一体机和200套 型一体机.(1)、求今年每套 型、 型一体机的价格各是多少万元(2)、该市明年计划采购 型、 型一体机1100套,考虑物价因素,预计明年每套 型一体机的价格比今年上涨25%,每套 型一体机的价格不变,若购买 型一体机的总费用不低于购买 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?23. 如图,点 是 的内心, 的延长线与 的外接圆 交于点 ,与 交于点 ,延长 、 相交于点 , 的平分线交 于点 . (1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.24. 如图1,在平面直角坐标系 中,已知抛物线 与 轴相交于 、 两点(点 在点 的左侧),与 轴交于点 .
(1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.24. 如图1,在平面直角坐标系 中,已知抛物线 与 轴相交于 、 两点(点 在点 的左侧),与 轴交于点 . (1)、点 的坐标为 , 点 的坐标为 , 线段 的长为 , 抛物线的解析式为.(2)、点 是线段 下方抛物线上的一个动点.
(1)、点 的坐标为 , 点 的坐标为 , 线段 的长为 , 抛物线的解析式为.(2)、点 是线段 下方抛物线上的一个动点.①如果在 轴上存在点 ,使得以点 、 、 、 为顶点的四边形是平行四边形.求点 的坐标.
②如图2,过点 作 交线段 于点 ,过点 作直线 交 于点 ,交 轴于点 ,记 ,求 关于 的函数解析式;当 取 和 时,试比较 的对应函数值 和 的大小.
