湖北省随州市2019年中考数学试卷

试卷更新日期：2019-08-14 类型：中考真卷

进入出卷网下载

一、单选题

1. -3的绝对值为（）

A、3 B、 $- 3$ C、 $\pm 3$ D、9

查看试题解析
2. 地球的半径约为6370000 $m$ ，用科学记数法表示正确的是（）

A、 $637 \times 10^{4} m$ B、 $63.7 \times 10^{5} m$ C、 $6.37 \times 10^{6} m$ D、 $6.37 \times 10^{7} m$

查看试题解析
3. 如图，直线 $l_{1} / / l_{2}$ ，直角三角板的直角顶点 $C$ 在直线 $l_{1}$ 上，一锐角顶点 $B$ 在直线 $l_{2}$ 上，若 ∠1=35° ，则 $∠ 2$ 的度数是（）

A、 $65^{\circ}$ B、 $55^{\circ}$ C、 $45^{\circ}$ D、 $35^{\circ}$

查看试题解析
4. 下列运算正确的是（）

A、 $4 m - m = 4$ B、 ${(a^{2})}^{3} = a^{5}$ C、 ${(x + y)}^{2} = x^{2} + y^{2}$ D、 $- (t - 1) = 1 - t$

查看试题解析
5. 某校男子篮球队10名队员进行定点投篮练习，每人投篮10次，他们投中的次数统计如表：

投中次数

3

5

6

7

8

人数

1

3

2

2

2

则这些队员投中次数的众数、中位数和平均数分别为（）

A、5，6，6 B、2，6，6 C、5，5，6 D、5，6，5

查看试题解析
6. 如图是一个几何体的三视图，则这个几何体的表面积为（）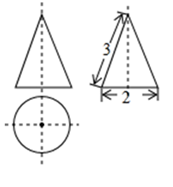

A、 $2 π$ B、 $3 π$ C、 $4 π$ D、 $5 π$

查看试题解析
7. 第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛，则下列函数图象可以体现这次比赛过程的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，在平行四边形 $A B C D$ 中， $E$ 为 $B C$ 的中点， $B D$ ， $A E$ 交于点 $O$ ，若随机向平行四边形 $A B C D$ 内投一粒米，则米粒落在图中阴影部分的概率为（）

A、 $\frac{1}{16}$ B、 $\frac{1}{12}$ C、 $\frac{1}{8}$ D、 $\frac{1}{6}$

查看试题解析
9. “分母有理化”是我们常用的一种化简的方法，如： $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 - \sqrt{3}) (2 + \sqrt{3})} = 7 + 4 \sqrt{3}$ ，除此之外，我们也可以用平方之后再开方的方式来化简一些有特点的无理数，如：对于 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，设 $x = \sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，易知 $\sqrt{3 + \sqrt{5}} > \sqrt{3 - \sqrt{5}}$ ，故 $x > 0$ ，由 $x^{2} = {(\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}})}^{2} = 3 + \sqrt{5} + 3 - \sqrt{5} - 2 \sqrt{(3 + \sqrt{5}) (3 - \sqrt{5})} = 2$ ，解得 $x = \sqrt{2}$ ，即 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}} = \sqrt{2}$ .根据以上方法，化简 $\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}} + \sqrt{6 - 3 \sqrt{3}} - \sqrt{6 + 3 \sqrt{3}}$ 后的结果为（）

A、 $5 + 3 \sqrt{6}$ B、 $5 + \sqrt{6}$ C、 $5 - \sqrt{6}$ D、 $5 - 3 \sqrt{6}$

查看试题解析
10. 如图所示，已知二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴交于 $A ， B$ 两点，与 $y$ 轴交于点 $C$ ， $O A = O C$ ，对称轴为直线 $x = 1$ ，则下列结论：① $a b c < 0$ ；② $a + \frac{1}{2} b + \frac{1}{4} c = 0$ ；③ $a c - b + 1 = 0$ ；④ $2 + c$ 是关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ 的一个根.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： ${(π - 2019)}^{0} - 2 \cos 60^{°} =$ .

查看试题解析
12. 如图，点 $A ， B ， C$ 在⊙ $O$ 上，点 $C$ 在优弧 $\overset{⌢}{A B}$ 上，若 $∠ O B A = 50^{\circ}$ ，则 $∠ C$ 的度数为.

查看试题解析
13. 2017年，随州学子尤东梅参加《最强大脑》节目，成功完成了高难度的项目挑战，展现了惊人的记忆力.在2019年的《最强大脑》节目中，也有很多具有挑战性的比赛项目，其中《幻圆》这个项目充分体现了数学的魅力.如图是一个最简单的二阶幻圆的模型，要求：①内、外两个圆周上的四个数字之和相等；②外圆两直径上的四个数字之和相等，则图中两空白圆圈内应填写的数字从左到右依次为和.

查看试题解析
14. 如图，在平面直角坐标系中， $R t Δ A B C$ 的直角顶点 $C$ 的坐标为 $(1 ， 0)$ ，点 $A$ 在 $x$ 轴正半轴上，且 $A C = 2$ .将 $Δ A B C$ 先绕点 $C$ 逆时针旋转 $90^{\circ}$ ，再向左平移3个单位，则变换后点 $A$ 的对应点的坐标为.

查看试题解析
15. 如图，矩形 $O A B C$ 的顶点 $A ， C$ 分别在 $y$ 轴、 $x$ 轴的正半轴上， $D$ 为 $A B$ 的中点，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象经过点 $D$ ，且与 $B C$ 交于点 $E$ ，连接 $O D$ ， $O E$ ， $D E$ ，若 $Δ O D E$ 的面积为3，则 $k$ 的值为.

查看试题解析

三、解答题

16. 解关于 $x$ 的分式方程： $\frac{9}{3 + x} = \frac{6}{3 - x}$ .

查看试题解析
17. 已知关于 $x$ 的一元二次方程 $x^{2} - (2 k + 1) x + k^{2} + 1 = 0$ 有两个不相等的实数根 $x_{1}, x_{2}$ .

(1)、求 $k$ 的取值范围；

(2)、若 $x_{1} + x_{2} = 3$ ，求 $k$ 的值及方程的根.

查看试题解析
18. “校园安全”越来越受到人们的关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题：

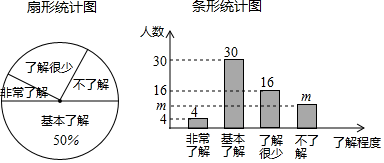(1)、接受问卷调查的学生共有人，条形统计图中m的值为；

(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为；

(3)、若该中学共有学生1800人，根据上述调查结果，可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为人；

(4)、若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛，请用列表或画树状图的方法，求恰好抽到1名男生和1名女生的概率.

查看试题解析
19. 在一次海上救援中，两艘专业救助船 $A ， B$ 同时收到某事故渔船的求救讯息，已知此时救助船 $B$ 在 $A$ 的正北方向，事故渔船 $P$ 在救助船 $A$ 的北偏西30°方向上，在救助船 $B$ 的西南方向上，且事故渔船 $P$ 与救助船 $A$ 相距120海里.

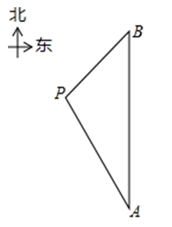(1)、求收到求救讯息时事故渔船 $P$ 与救助船 $B$ 之间的距离；

(2)、若救助船A ， $B$ 分别以40海里/小时、30海里/小时的速度同时出发，匀速直线前往事故渔船 $P$ 处搜救，试通过计算判断哪艘船先到达.

查看试题解析
20. 如图，在 $Δ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的⊙ $O$ 分别交 $A C ， B C$ 于点 $D ， E$ ，点 $F$ 在 $A C$ 的延长线上，且 $∠ B A C = 2 ∠ C B F$ .

(1)、求证： $B F$ 是⊙ $O$ 的切线；

(2)、若⊙ $O$ 的直径为3， $\sin ∠ C B F = \frac{\sqrt{3}}{3}$ ，求 $B C$ 和 $B F$ 的长.

查看试题解析
21. 某食品厂生产一种半成品食材，成本为2元/千克，每天的产量 $p$ （百千克）与销售价格 $x$ （元/千克）满足函数关系式 $p = \frac{1}{2} x + 8$ ，从市场反馈的信息发现，该半成品食材每天的市场需求量 $q$ （百千克）与销售价格 $x$ （元/千克）满足一次函数关系，部分数据如表：

销售价格 $x$ （元/千克）

2

4

……

10

市场需求量 $q$ （百千克）

12

10

……

4

已知按物价部门规定销售价格 $x$ 不低于2元/千克且不高于10元/千克.

(1)、直接写出 $q$ 与 $x$ 的函数关系式，并注明自变量 $x$ 的取值范围；

(2)、当每天的产量小于或等于市场需求量时，这种半成品食材能全部售出，而当每天的产量大于市场需求量时，只能售出符合市场需求量的半成品食材，剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时，求 $x$ 的取值范围；

②求厂家每天获得的利润y（百元）与销售价格 $x$ 的函数关系式；

(3)、在（2）的条件下，当 $x$ 为元/千克时，利润 $y$ 有最大值；若要使每天的利润不低于24（百元），并尽可能地减少半成品食材的浪费，则 $x$ 应定为元/千克.

查看试题解析
22. 若一个两位数十位、个位上的数字分别为 $m ， n$ ，我们可将这个两位数记为 $m n$ ，易知 $m n = 10 m + n$ ；同理，一个三位数、四位数等均可以用此记法，如 $a b c = 100 a + 10 b + c$ .

(1)、【基础训练】
解方程填空：
①若 $2 x + x 3 = 45$ ，则 $x =$ ；

②若 $7 y - y 8 = 26$ ，则 $y =$ ；

③若 $t 93 + 5 t 8 = 13 t 1$ ，则 $t =$ ；

(2)、【能力提升】
交换任意一个两位数 $m n$ 的个位数字与十位数字，可得到一个新数 $n m$ ，则 $m n + n m$ 一定能被整除， $m n - n m$ 一定能被整除， $m n • n m - m n$ 一定能被整除；（请从大于5的整数中选择合适的数填空）

(3)、【探索发现】
北京时间2019年4月10日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力极大的天体，连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象：任选一个三位数，要求个、十、百位的数字各不相同，把这个三位数的三个数字按大小重新排列，得出一个最大的数和一个最小的数，用得出的最大的数减去最小的数得到一个新数（例如若选的数为325，则用532-235=297），再将这个新数按上述方式重新排列，再相减，像这样运算若干次后一定会得到同一个重复出现的数，这个数称为“卡普雷卡尔黑洞数”.
①该“卡普雷卡尔黑洞数”为；

②设任选的三位数为 $a b c$ （不妨设 $a > b > c$ ），试说明其均可产生该黑洞数.

查看试题解析

销售价格 $x$ （元/千克）	2	4	……	10
市场需求量 $q$ （百千克）	12	10	……	4

投中次数	3	5	6	7	8
人数	1	3	2	2	2