贵州省铜仁市2019年中考数学试卷
试卷更新日期:2019-08-14 类型:中考真卷
一、单选题
-
1. 2019的相反数是( )A、 B、﹣ C、|2019| D、﹣20192. 如图,如果∠1=∠3,∠2=60°,那么∠4的度数为( )
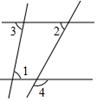 A、60° B、100° C、120° D、130°3. 今年我市参加中考的学生约为56000人,56000用科学记数法表示为( )A、56×103 B、5.6×104 C、0.56×105 D、5.6×10﹣44. 某班17名女同学的跳远成绩如下表所示:
A、60° B、100° C、120° D、130°3. 今年我市参加中考的学生约为56000人,56000用科学记数法表示为( )A、56×103 B、5.6×104 C、0.56×105 D、5.6×10﹣44. 某班17名女同学的跳远成绩如下表所示:成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
这些女同学跳远成绩的众数和中位数分别是( )
A、1.70,1.75 B、1.75,1.70 C、1.70,1.70 D、1.75,1.7255. 如图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( ) A、360° B、540° C、630° D、720°6. 一元二次方程4x2﹣2x﹣1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根7. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )
A、360° B、540° C、630° D、720°6. 一元二次方程4x2﹣2x﹣1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根7. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )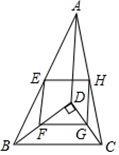 A、12 B、14 C、24 D、218. 如图,四边形ABCD为菱形,AB=2,∠DAB=60°,点E,F分别在边DC,BC上,且CE= CD,CF= CB,则S△CEF=( )
A、12 B、14 C、24 D、218. 如图,四边形ABCD为菱形,AB=2,∠DAB=60°,点E,F分别在边DC,BC上,且CE= CD,CF= CB,则S△CEF=( )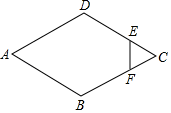 A、 B、 C、 D、9. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )
A、 B、 C、 D、9. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )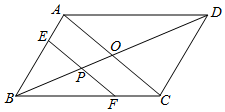 A、
A、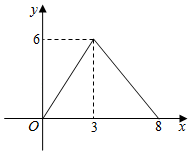 B、
B、 C、
C、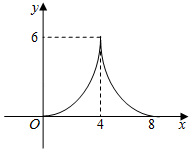 D、
D、 10. 如图,正方形ABCD中,AB=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G,FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED;②△DFG≌△DCG;③△FHB∽△EAD;④tan∠GEB= ;⑤S△BFG=2.6;其中正确的个数是( )
10. 如图,正方形ABCD中,AB=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G,FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED;②△DFG≌△DCG;③△FHB∽△EAD;④tan∠GEB= ;⑤S△BFG=2.6;其中正确的个数是( )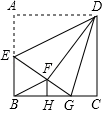 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 因式分解:a2-9=.12. 小刘和小李参加射击训练,各射击10次的平均成绩相同,如果他们射击成绩的方差分别是S小刘2=0.6,S小李2=1.4,那么两人中射击成绩比较稳定的是;13. 如图,四边形ABCD为⊙O的内接四边形,∠A=100°,则∠DCE的度数为;
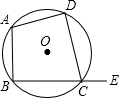 14. 分式方程 的解为y=.15. 某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为.16. 如图,在△ABC中,D是AC的中点,且BD⊥AC,ED∥BC,ED交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于cm.
14. 分式方程 的解为y=.15. 某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为.16. 如图,在△ABC中,D是AC的中点,且BD⊥AC,ED∥BC,ED交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于cm.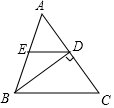 17. 如果不等式组 的解集是x<a﹣4,则a的取值范围是.18. 按一定规律排列的一列数依次为: , , , ,…(a≠0),按此规律排列下去,这列数中的第n个数是.(n为正整数)
17. 如果不等式组 的解集是x<a﹣4,则a的取值范围是.18. 按一定规律排列的一列数依次为: , , , ,…(a≠0),按此规律排列下去,这列数中的第n个数是.(n为正整数)三、解答题
-
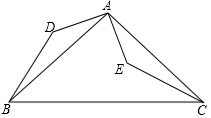
19.(1)、计算:|﹣ |+(﹣1)2019+2sin30°+( ﹣ )0(2)、先化简,再求值: ,其中x=﹣220. 如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.
求证:BD=CE.
 21. 某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
21. 某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):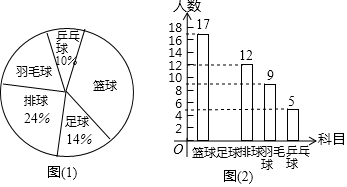 (1)、请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);(2)、在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?22. 如图,A、B两个小岛相距10km,一架直升飞机由B岛飞往A岛,其飞行高度一直保持在海平面以上的hkm,当直升机飞到P处时,由P处测得B岛和A岛的俯角分别是45°和60°,已知A、B、P和海平面上一点M都在同一个平面上,且M位于P的正下方,求h(结果取整数, ≈1.732)
(1)、请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);(2)、在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?22. 如图,A、B两个小岛相距10km,一架直升飞机由B岛飞往A岛,其飞行高度一直保持在海平面以上的hkm,当直升机飞到P处时,由P处测得B岛和A岛的俯角分别是45°和60°,已知A、B、P和海平面上一点M都在同一个平面上,且M位于P的正下方,求h(结果取整数, ≈1.732)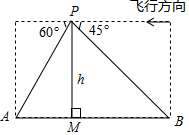 23. 如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数 的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
23. 如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数 的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.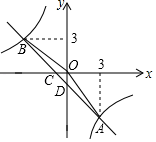 (1)、求一次函数的表达式;(2)、求△AOB的面积;(3)、写出不等式kx+b>﹣ 的解集.24. 如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)、求一次函数的表达式;(2)、求△AOB的面积;(3)、写出不等式kx+b>﹣ 的解集.24. 如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.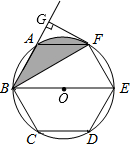 (1)、求证:FG是⊙O的切线;(2)、已知FG=2 ,求图中阴影部分的面积.25. 如图,已知抛物线y=ax2+bx﹣1与x轴的交点为A(﹣1,0),B(2,0),且与y轴交于C点.
(1)、求证:FG是⊙O的切线;(2)、已知FG=2 ,求图中阴影部分的面积.25. 如图,已知抛物线y=ax2+bx﹣1与x轴的交点为A(﹣1,0),B(2,0),且与y轴交于C点.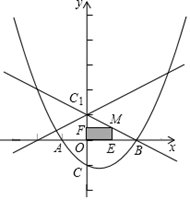 (1)、求该抛物线的表达式;(2)、点C关于x轴的对称点为C1 , M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由.(3)、已知点P是直线y= x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
(1)、求该抛物线的表达式;(2)、点C关于x轴的对称点为C1 , M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由.(3)、已知点P是直线y= x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.