2017年江苏省南京市六区联考中考数学一模试卷

试卷更新日期：2017-06-20 类型：中考模拟

进入出卷网下载

一、选择题

1. 计算|﹣4+1|的结果是（）

A、﹣5 B、﹣3 C、3 D、5

查看试题解析
2. 计算（﹣xy²）³的结果是（）

A、x³y⁶ B、﹣x³y⁶ C、﹣x⁴y⁵ D、x⁴y⁵

查看试题解析
3. 与 $\sqrt{17}$ 最接近的整数为（）

A、2 B、3 C、4 D、5

查看试题解析
4. 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁ ， l₂ ， l₃于点A，B，C；直线DF分别交l₁ ， l₂ ， l₃于点D，E，F．AC与DF相交于点H，且AH=2，HB=1，BC=5，则 $\frac{D E}{E F}$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
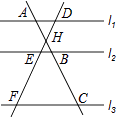5. 若一组数据2、4、6、8、x的方差比另一组数据5、7、9、11、13的方差大，则 x 的值可以为（）

A、12 B、10 C、2 D、0

查看试题解析
6. 如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（）

A、48 B、50 C、54 D、60

查看试题解析

二、填空题

7. 9的平方根是；9的立方根是．

查看试题解析
8. 若使 $\sqrt{x + 1}$ 有意义，则x的取值范围是．

查看试题解析
9. 2016年南京全市完成全社会固定资产投资约55000000万元，将55000000用科学记数法表示为．

查看试题解析
10. 分解因式x³+6x²+9x= ．

查看试题解析
11. 计算 $\frac{3}{\sqrt{3}}$ ﹣ $\sqrt{\frac{1}{3}}$ 的结果是．

查看试题解析
12. 已知关于x的方程x²﹣3x+m=0的一个根是2，则它的另一个根是， m的值是．

查看试题解析
13. 如图，∠A=∠C，只需补充一个条件：，就可得△ABD≌△CDB．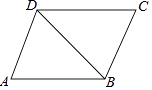

查看试题解析
14. 如图，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O，若∠BAC等于82°，则∠OBC=°．

查看试题解析
15. 已知点A（﹣1，﹣2）在反比例函数y= $\frac{k}{x}$ 的图象上，则当x＞1时，y的取值范围是．

查看试题解析
16. =如图，在半径为2的⊙O中，弦AB=2，⊙O上存在点C，使得弦AC=2 $\sqrt{2}$ ，则∠BOC=°．

查看试题解析

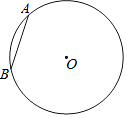
三、解答题

17. 解不等式组 ${\begin{matrix} x + 1 \geq 0 \\ \frac{x - 1}{2} < \frac{x}{3} \end{matrix}$ ，并写出它的整数解．

查看试题解析
18. 化简：（ $\frac{2 m}{m^{2} - 4}$ ﹣ $\frac{1}{m + 2}$ ）÷ $\frac{1}{m^{2} - 2 m}$ ．

查看试题解析
19.
在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图．请根据相关信息，解答下列问题：

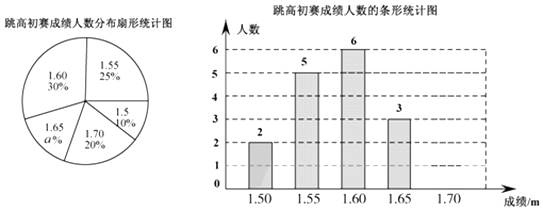(1)、扇形统计图中a= ，初赛成绩为1.70m所在扇形图形的圆心角为°；

(2)、补全条形统计图；

(3)、这组初赛成绩的众数是 m，中位数是 m；

(4)、根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？

查看试题解析
20. 在一个不透明袋子中有1个红球、1 个绿球和n个白球，这些球除颜色外都相同．

(1)、从袋中随机摸出1个球，记录下颜色后放回袋子中并搅匀，不断重复该试验．发现摸到白球的频率稳定在0.75，则n的值为；

(2)、当n=2时，把袋中的球搅匀后任意摸出2个球，求摸出的2个球颜色不同的概率．

查看试题解析
21. 如图，将矩形ABCD绕点C旋转得到矩形FECG，点E在AD上，延长ED交FG于点H．

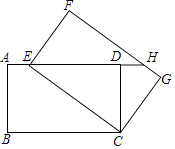(1)、求证：△EDC≌△HFE；

(2)、连接BE、CH．四边形BEHC是怎样的特殊四边形？证明你的结论．

(3)、连接BE、CH．当AB与BC的比值为时，四边形BEHC为菱形．

查看试题解析
22. 据大数据统计显示，某省2014年公民出境旅游人数约100万人次，2015年与2016年两年公民出境旅游总人数约264万人次．若这两年公民出境旅游总人数逐年递增，请解答下列问题：

(1)、求这两年该省公民出境旅游人数的年平均增长率；

(2)、如果2017年仍保持相同的年平均增长率，请你预测2017年该省公民出境旅游人数约多少万人次？

查看试题解析
23. 如图，小明要测量河内小岛B到河边公路AD的距离，在点A处测得∠BAD=37°，沿AD方向前进150米到达点C，测得∠BCD=45°．求小岛B到河边公路AD的距离．
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
24. 已知二次函数y=x²﹣2mx+m²+m+1的图象与x轴交于A、B两点，点C为顶点．

(1)、求m的取值范围；

(2)、若将二次函数的图象关于x轴翻折，所得图象的顶点为D，若CD=8．求四边形ACBD的面积．

查看试题解析
25. 已知：如图，已知⊙O的半径为1，菱形ABCD的三个顶点A、B、D在⊙O上，且CD与⊙O相切．

(1)、求证：BC与⊙O相切；

(2)、求阴影部分面积．

查看试题解析
26. 甲、乙两人周末从同一地点出发去某景点，因乙临时有事，甲坐地铁先出发，甲出发0.2小时后乙开汽车前往．设甲行驶的时间为x（h），甲、乙两人行驶的路程分别为y₁（km）与y₂（km）．如图①是y₁与y₂关于x的函数图象．

(1)、分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式；

(2)、当x为多少时，两人相距6km？

(3)、设两人相距S千米，在图②所给的直角坐标系中画出S关于x的函数图象．

查看试题解析
27. 解决问题时需要思考：是否解决过与其类似的问题．小明从问题1解题思路中获得启发从而解决了问题2．

(1)、问题1：如图①，在正方形ABCD中，E、F是BC、CD上两点，∠EAF=45°．
求证：∠AEF=∠AEB．
小明给出的思路为：延长EB到H，满足BH=DF，连接AH．请完善小明的证明过程．

(2)、问题2：如图②，在等腰直角△ABC中，∠ACB=90°，AC=BC=4，D为AB中点，E、F是AC、BC边上两点，∠EDF=45°．
①求点D到EF的距离．
②若AE=a，则S_△_DEF=（用含字母a的代数式表示）．

查看试题解析