2017年吉林省延边州中考数学模拟试卷

试卷更新日期：2017-06-20 类型：中考模拟

进入出卷网下载

一、单项选择题

1. 下列各数中最小的数是（）

A、0 B、3 C、﹣ $\sqrt{3}$ D、1

查看试题解析
2. 2016年10月17日，神舟十一号飞船成功发射升空．发射当天约有161000个相关精彩栏目的热门视频在网络上热播．将数据161000用科学记数法表示为（）

A、1.61×10³ B、0.161×10⁵ C、1.61×10⁵ D、16.1×10⁴

查看试题解析
3. 用4个完全相同的小正方体组合成如图所示的立体图形，它的左视图为（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、2a²•a=3a³ B、（2a）²÷a=4a C、（﹣3a）²=3a² D、（a﹣b）²=a²﹣b²

查看试题解析
5. 将一副三角板如图方式放置，则∠1的度数是（）

A、15° B、20° C、25° D、30°

查看试题解析
6. A，B两地相距180km，新修的高速公路开通后，在A，B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h．若设原来的平均车速为xkm/h，则根据题意可列方程为（）

A、 $\frac{180}{x}$ ﹣ $\frac{180}{(1 + 50 %) x}$ =1 B、 $\frac{180}{(1 + 50 %) x}$ ﹣ $\frac{180}{x}$ =1 C、 $\frac{180}{x}$ ﹣ $\frac{180}{(1 - 50 %) x}$ =1 D、 $\frac{180}{(1 - 50 %) x}$ ﹣ $\frac{180}{x}$ =1

查看试题解析

二、填空题

7. 计算： $\sqrt{12}$ + $\sqrt{3}$ = ．

查看试题解析
8. 因式分解：m²﹣4n²= ．

查看试题解析
9. 不等式5x＞2x﹣6的解集是．

查看试题解析
10. 若x²﹣6x+7=（x﹣3）²+n，则n= ．

查看试题解析
11. 若两个连续整数x、y满足x＜ $\sqrt{5}$ +1＜y，则x+y的值是．

查看试题解析
12. 夏天某地区一周最高气温的走势图如图所示，这组数据的众数是℃．

查看试题解析
13. 如图，某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形，则扇形的圆心角∠DAB的度数是度．（结果保留π）

查看试题解析
14. 如图，线段OA=4，点C是OA的中点，以线段CA为对角线作正方形ABCD．将线段OA绕点O向逆时针方向旋转60°，得到线段OA′和正方形A′B′C′D′．在旋转过程中，正方形ABCD扫过的面积是．（结果保留π）

查看试题解析

三、解答题

15. 先化简，再求值：（1+x）（1﹣x）+x（x+2）﹣1，其中x= $\frac{1}{2}$ ．

查看试题解析
16. 如图所示的两台天平保持平衡，已知每块巧克力的质量相等，且每个果冻的质量也相等．求每块巧克力和每个果冻的质量．

查看试题解析
17. 在一个不透明的袋子中，装有2个红球和1个白球，这些球除了颜色外都相同．如果第一次随机摸出一个小球（不放回），充分搅匀后，第二次再从剩余的两球中随机摸出一个小球，求两次都摸到红球的概率．（用树状图或列表法求解）

查看试题解析
18. 如图，已知△ABC中，AB=AC，把△ABC绕A点顺时针方向旋转得到△ADE，连接BD，CE交于点F，求证：△AEC≌△ADB．

查看试题解析

四、解答题

19. 如图所示，网格中每个小正方形的边长为1，请你认真观察图（1）中的三个网格中阴影部分构成的图案，解答下列问题：

(1)、这三个图案都具有以下共同特征：都是对称图形，都不是对称图形．

(2)、请在图（2）中设计出一个面积为4，且具备上述特征的图案，要求所画图案不能与图（1）中所给出的图案相同．

查看试题解析
20. 为了解某市12000名初中学生的视力情况，该校数学兴趣小组从该市七、八、九年级各随机抽取了100名学生进行调查，整理他们的视力情况数据，得到如下的折线统计图．

(1)、由统计图可以看出年级越高视力不良率越（填“高”或“低”）；

(2)、抽取的八年级学生中，视力不良的学生有名；

(3)、请你根据抽样调查的结果，估计该市12000名初中学生中视力不良的人数是多少？

查看试题解析
21. 保护视力要求人写字时眼睛和笔端的距离应超过30cm，图1是一位同学的坐姿，把他的眼睛B，肘关节C和笔端A的位置关系抽象成图2的△ABC，已知BC=30cm，AC=22cm，∠ACB=53°，他的这种坐姿符合保护视力的要求吗？请说明理由．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3）

查看试题解析
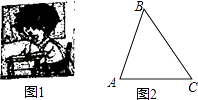22.
如图，在平面直角坐标系中有Rt△ABC，已知∠CAB=90°，AB=AC，A（﹣2，0），B（0，1）．

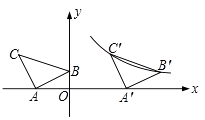(1)、点C的坐标是；

(2)、将△ABC沿x轴正方向平移得到△A′B′C′，且B，C两点的对应点B′，C′恰好落在反比例函数y= $\frac{k}{x}$ 的图象上，求该反比例函数的解析式．

查看试题解析

五、解答题

23. 如图，⊙O的直径AB=4，C是⊙O上一点，连接OC．过点C作CD⊥AB，垂足为D，过点B作BM∥OC，在射线BM上取点E，使BE=BD，连接CE．

(1)、当∠COB=60°时，直接写出阴影部分的面积；

(2)、求证：CE是⊙O的切线．

查看试题解析
24. 某商场为了迎接“6.1儿童节“，以调低价格的方式促销n个不同的玩具，调整后的单价y（元）与调整前的单价x（元）满足一次函数关系，如表：
第1个
第2个
第3个
第4个
…
第n个
调整前单价x （元）
x1
x2=6
x3=72
x4
…
xn
调整后单价y （元）
y1
y2=4
y3=59
y4
…
yn
当这些玩具调整后的单价都大于2元时，解答下列问题：

(1)、y与x的函数关系式为，x的取值范围为；

(2)、某个玩具调整前单价是108元，顾客购买这个玩具省了元；

(3)、这n个玩具调整前、后的平均单价分别为 $\bar{x}$ （元）、 $\bar{y}$ （元），猜想 $\bar{y}$ 与 $\bar{x}$ 的关系式，并写出推导过程．

查看试题解析

六、解答题

25.
如图，点A、B的坐标分别为（4，0）、（0，8），点C是线段OB上一动点，点E在x轴正半轴上，四边形OEDC是矩形，且OE=2OC．设OE=t（t＞0），矩形OEDC与△AOB重合部分的面积为S．
根据上述条件，回答下列问题：

(1)、当矩形OEDC的顶点D在直线AB上时，求t的值；

(2)、当t=4时，求S的值；

(3)、直接写出S与t的函数关系式（不必写出解题过程）；

(4)、若S=12，则t= ．

查看试题解析
26.
问题情景：
如图，在直角坐标系xOy中，点A、B为二次函数y=ax²（a＞0）图象上的两点，且点A、B的横坐标分别为m、n（m＞n＞0），连接OA、AB、OB．设△AOB的面积为S时，解答下列问题：

(1)、探究：当a=1时，

mn
m﹣n
S
m=3，n=1
3
2
m=5，n=2
10
3
当a=2时，

2mn
m﹣n
S
m=3，n=1
6
2
m=5，n=2
20
3

(2)、归纳证明：对任意m、n（m＞n＞0），猜想S=（用a，m，n表示），并证明你的猜想．

(3)、拓展应用：
若点A、B的横坐标分别为m、n（m＞0＞n），其它条件不变时，△AOB的面积S=（用a，m，n表示）．

查看试题解析

	第1个	第2个	第3个	第4个	…	第n个
调整前单价x （元）	x1	x2=6	x3=72	x4	…	xn
调整后单价y （元）	y1	y2=4	y3=59	y4	…	yn

	mn	m﹣n	S
m=3，n=1	3	2
m=5，n=2	10	3

	2mn	m﹣n	S
m=3，n=1	6	2
m=5，n=2	20	3