2017年湖北省黄冈市中考数学模拟试卷（一）
试卷更新日期：2017-06-20 类型：中考模拟
一、选择题
-
1. 化简 等于（ ）A、±2 B、2 C、﹣2 D、2. 要使分式 有意义，则x的取值应满足（ ）A、x≥3 B、x＜﹣3 C、x≠﹣3 D、x≠33. 下列计算结果为x6的是（ ）A、x•x6 B、（x2）3 C、（2x2）3 D、（x3）4÷x24. 袋中装有4个红球和2个黄球，这些球的形状、大小、质地完全相同，在看不到球的条件下，随机地从袋子中摸出三个球，下列事件是不可能事件的是（ ）A、摸出的三个球中至少有一个红球 B、摸出的三个球中有两个球是黄球 C、摸出的三个球都是红球 D、摸出的三个球都是黄球5. 计算（a﹣1）2正确的是（ ）A、a2﹣a+1 B、a2﹣2a+1 C、a2﹣2a﹣1 D、a2﹣16. 在平面直角坐标系中，将点A（x，y）向左平移5个单位长度，再向上平移3个单位长度后与点B（﹣3，2）重合，则点A的坐标是（ ）A、（2，5） B、（﹣8，5） C、（﹣8，﹣1） D、（2，﹣1）7. 如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，则其主视图可能是（ ）
A、
B、
C、
D、
8. 在2017年体育中考中，某班一学习小组8名学生的体育成绩如下表，则这组学生的体育成绩的众数，中位数、平均数依次是（ ）成绩分数
27
28
30
人数
4
3
1
A、28 27.5 27.75 B、27 27.5 27.75 C、28 27 27.7 D、27 28 27.759.如图：直线l：y=﹣x，点A1的坐标为（﹣1，0），过点A1作x轴的垂线交直线l于点B1 ， 以原点O为圆心，OB1长为半径画弧交x轴负半轴于点A2 ， 再过点A2作x轴的垂线交直线l于点B2 ， 以原点O为圆心，OB2长为半径画弧交x轴负半轴于点A3…按此作法进行去，点A2016的坐标为（ ）
A、（﹣22016 ， 0） B、（﹣22017 ， 0） C、（﹣21008 ， 0） D、（﹣21007 ， 0）10. 已知二次函数y=x2+2x+m2+2m﹣1（m为常数），当自变量x的值满足1≤x≤3时，与其对应的函数值y的最小值为5，则m的值为（ ）A、1或﹣5 B、﹣1或5 C、1或﹣3 D、1或3二、填空题
-
11. 计算2﹣（﹣4）= ．12. 计算： = ．13. 学校为了了解九年级学生“一分钟跳绳次数”的情况，随机选取了4名女生和2名男生，则从这6名学生中选取2名同时跳绳，恰好选中一男一女的概率是 ．14. 如图，在菱形ABCD中，∠BAD=120°，点E、F分别在边AB、BC上，△BEF与△GEF关于直线EF对称，点B的对称点是G，且点G在边AD上，若EG⊥AC，AB=2，则FG的长为 ．
15. 如图，已知点A（1，2）是反比例函数y= 图象上的一点，连接AO并延长交双曲线的另一分支于点B，点P是x轴上一动点；若△PAB是等腰三角形，则点P的坐标是 ．
16. 如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为 ．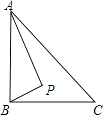
三、解答题
-
17. 解方程： +1=x﹣ ．18. 如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：BE=CD．
19. 某市三景区是人们节假日游玩的热点景区，某学校对九（1）班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查，调查分四个类别，A：三个景区；B：游两个景区；C：游一个景区；D：不到这三个景区游玩，现根据调查结果绘制了不完全的条形统计图和扇形统计图如下：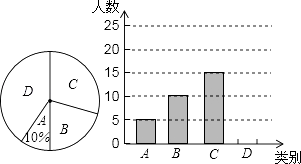
请结合图中信息解答下列问题：
(1)、九（1）班现有学生人，在扇形统计图中表示“B类别”的扇形的圆心角的度数为；(2)、请将条形统计图补充完整；(3)、若该校九年级有1000名学生，求计划“五一”小长假随父母到这三个景区游玩的学生多少名？
