2017年黑龙江省哈尔滨市香坊区中考数学一模试卷
试卷更新日期：2017-06-20 类型：中考模拟
一、选择题
-
1. 下列各对数是互为倒数的是（ ）A、4和﹣4 B、﹣3和 C、﹣2和 D、0和02. 下列运算正确的是（ ）A、a2•a3=a6 B、（a2）3=a5 C、（2a+1）2=4a2+1 D、（﹣2a2b）3=﹣8a6b33. 在下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
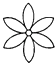D、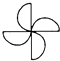
4. 如图是由5个相同的小正方体构成的几何体，其主视图是（ ）
A、
B、
C、
D、
5. 反比例函数y= 的图象，当x＞0时，y随x的增大而增大，则k的取值范围是（ ）A、k＜3 B、k≤3 C、k＞3 D、k≥36. 对于二次函数y=﹣ （x﹣2）2﹣3，下列说法错误的是（ ）A、图象的开口向下 B、当x=2时，y有最大值﹣3 C、图象的顶点坐标为（2，﹣3） D、图象与y轴的交点坐标为（0，﹣3）7.如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进40海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD是（ ）
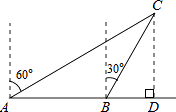A、20海里 B、40海里 C、20 海里 D、40 海里8. 如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，则下列结论错误的是（ ）
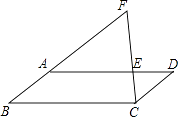A、EF=2CE B、S△AEF= S△BCF C、BF=3CD D、BC= AE9. “五一节”期间，王老师一家自驾游去了离家170千米的某地，下面是他们家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象，当他们离目的地还有20千米时，汽车一共行驶的时间是（ ）
A、2小时 B、2.2小时 C、2.25小时 D、2.4小时二、填空题
-
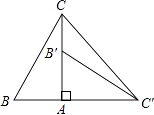
10. 12000用科学记数法表示为 ．11. 在函数y= 中，自变量x的取值范围是12. 计算 ﹣3 的结果是 ．13. 把多项式2mx2﹣4mxy+2my2分解因式的结果是 ．14. 不等式组 的解集是 ．15. 如图，在Rt△ABC中，∠BAC=90°，∠B=60°，△AB′C′可以由△ABC绕点A顺时针旋转90°得到（点B′与点B是对应点，点C′与点C是对应点），连接CC′，则∠CC′B′的度数是 ．
16. 已知等边三角形ABC的边长为8，P是BC边上一点，连接AP，若AP=7，则BP的长为 ．17. 一个布袋内只装有1个黑球和2个白球，这些球除颜色外其余都相同，随机摸出一个球后放回搅匀，再随机摸出一个球，则两次摸出的球都是黑球的概率是 ．18. 如图，PA、PB是⊙O的两条切线，A、B是切点，PA= OA，阴影部分的面积为6π，则⊙O的半径长为 ．
19. 如图，在△ABC中，∠ACB=90°，AC=BC，D是△ABC外一点，连接AD、BD、CD，若∠CDB=90°，BD=3，AD= ，则AC长为 ．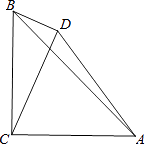
三、解答题
-
20. 先化简，再求代数式 的值，其中x=4sin45°﹣2cos60°．21.
图1、图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．
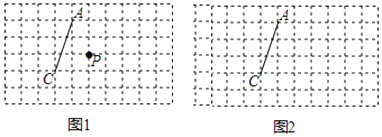(1)、如图1，点P在小正方形的顶点上，在图1中作出点P关于直线AC的对称点Q，连接AQ、QC、CP、PA，并直接写出四边形AQCP的周长；(2)、在图2中画出一个以线段AC为一条对角线、面积为15的菱形ABCD，且点B和点D均在小正方形的顶点上．22. 我市某中学为了解该校学生对四种国家一级保护动物的喜爱情况，围绕“在丹顶鹤、大熊猫、滇金丝猴、藏羚羊四种国家一级保护动物中，你最喜欢哪一种动物？（必选且只选一种）”这一问题，在全校范围内随机抽取部分同学进行问卷调查．根据调查结果绘制成如下不完整的条形统计图．其中最喜欢丹顶鹤的学生人数占被抽取人数的16%；请你根据以上信息解答下列问题：
(1)、在这次调查中，一共抽取了多少名学生？(2)、求在被调查的学生中，最喜欢滇金丝猴的学生有多少名？并补全条形统计图；(3)、如果全校有1200名学生，请你估计全校最喜欢大熊猫的学生有多少名？23. 在△ABC中，∠C=90°，D是AC的中点，E是AB的中点，作EF⊥BC于F，延长BC至G，使CG=BF，连接CE、DE、DG．(1)、如图1，求证：四边形CEDG是平行四边形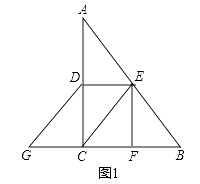
；(2)、如图2，连接EG交AC于点H，若EG⊥AB，请直接写出图2中所有长度等于 GH的线段．
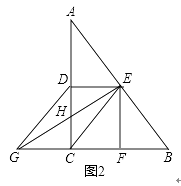24. 某校为美化校园，计划对面积为1800平方米的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400平方米区域的绿化时，甲队比乙队少用4天．(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少平方米？(2)、若学校每天付给乙队的绿化费用是0.25万元，每天付给甲队的绿化费用比乙队多60%，要使这次学校付给甲、乙两队的绿化总费用不超过8万元，至少应安排甲队工作多少天？25. 已知，⊙O的两条弦AB、CD相交于点E，(1)、如图1，若BE=DE，求证： = ；
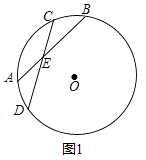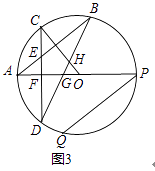
(2)、如图2，在（1）的条件下，连接OC，AP为⊙O的直径，PQ为⊙O的弦，且PQ∥AB，求证：∠OCD=∠APQ；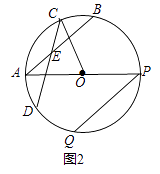
(3)、如图3，在（2）的条件下，连接BD分别与OA、OC交于点G、H，连接DQ，设CD与AP交于点F，若PQ=2CF，BH=5GH，DQ=4，求⊙O的半径．
26.如图，在平面直角坐标系中，O为坐标原点，直线y=﹣x﹣3与x轴交于点A，与y轴交于点C，抛物线y=x2+bx+c经过A、C两点，与x轴交于另一点B
(1)、求抛物线的解析式；(2)、点D是第二象限抛物线上的一个动点，连接AD、BD、CD，当S△ACD= S四边形ACBD时，求D点坐标；(3)、在（2）的条件下，连接BC，过点D作DE⊥BC，交CB的延长线于点E，点P是第三象限抛物线上的一个动点，点P关于点B的对称点为点Q，连接QE，延长QE与抛物线在A、D之间的部分交于一点F，当∠DEF+∠BPC=∠DBE时，求EF的长．