2017年山东省泰安市岱岳区中考数学模拟试卷(3月份)
试卷更新日期:2017-06-20 类型:中考模拟
一、选择题
-
1. 若a是最大的负整数,b是绝对值最小的有理数,c是倒数等于它本身的自然数,则代表式a2015+2016b+c2017的值为( )A、2015 B、2016 C、2017 D、02. 已知非零实数a,b,满足|3a﹣4|+|b+2|+ +4=3a,则a+b等于( )A、﹣1 B、9 C、1 D、23. 求1+2+22+23…+22012的值,可令S=1+2+22+23+…+22012 , 则2S=2+22+23+24+…+22013 , 因此2S﹣S=22013﹣1,仿照以上推理,计算出1+5+52+53+…+52017的值为( )A、52017﹣1 B、52018﹣1 C、 D、4. 已知实数x,y,z满足 ,则代数式4x﹣4z+1的值是( )A、﹣3 B、3 C、﹣7 D、75. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
 A、 B、 C、 D、6. 已知:a=2014x+2015,b=2014x+2016,c=2014x+2017,则a2+b2+c2﹣ab﹣ac﹣bc的值是( )A、0 B、1 C、2 D、37. 如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
A、 B、 C、 D、6. 已知:a=2014x+2015,b=2014x+2016,c=2014x+2017,则a2+b2+c2﹣ab﹣ac﹣bc的值是( )A、0 B、1 C、2 D、37. 如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( ) A、8 B、8 C、2 D、108. 由若干个相同小正方体组合成一个几何体,使组合几何体的主视图、俯视图如图所示.这样的组合几何体不只有一种,它的组成最少需要x个小正方体,最多需要y个小正方体.则y﹣x的值为( )
A、8 B、8 C、2 D、108. 由若干个相同小正方体组合成一个几何体,使组合几何体的主视图、俯视图如图所示.这样的组合几何体不只有一种,它的组成最少需要x个小正方体,最多需要y个小正方体.则y﹣x的值为( ) A、4 B、3 C、2 D、19. 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
A、4 B、3 C、2 D、19. 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( ) A、68° B、88° C、90° D、112°10. △ABC中,∠ACB=90°,∠A=α,以C为中心将△ABC旋转θ角到△A1B1C(旋转过程中保持△ABC的形状大小不变)B点恰落在A1B1上,如图,则旋转角θ的大小为( )
A、68° B、88° C、90° D、112°10. △ABC中,∠ACB=90°,∠A=α,以C为中心将△ABC旋转θ角到△A1B1C(旋转过程中保持△ABC的形状大小不变)B点恰落在A1B1上,如图,则旋转角θ的大小为( ) A、α+10° B、α+20° C、α D、2α11. 已知关于x的不等式组 恰有3个整数解,则a的取值范围是()A、 B、 C、 D、12. 山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )A、140元 B、150元 C、160元 D、180元13.
A、α+10° B、α+20° C、α D、2α11. 已知关于x的不等式组 恰有3个整数解,则a的取值范围是()A、 B、 C、 D、12. 山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )A、140元 B、150元 C、160元 D、180元13.如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
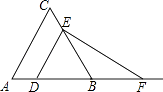 A、
A、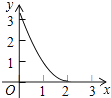 B、
B、 C、
C、 D、
D、 14. 如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为()
14. 如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为() A、(﹣ , ) B、(﹣ , ) C、(﹣ , ) D、(﹣ , )15. 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )
A、(﹣ , ) B、(﹣ , ) C、(﹣ , ) D、(﹣ , )15. 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )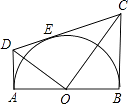 A、2个 B、3个 C、4个 D、5个16. 如图,在直角△BAD中,延长斜边BD到点C,使DC= BD,连接AC,若tanB= ,则tan∠CAD的值( )
A、2个 B、3个 C、4个 D、5个16. 如图,在直角△BAD中,延长斜边BD到点C,使DC= BD,连接AC,若tanB= ,则tan∠CAD的值( ) A、 B、 C、 D、17. 如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )
A、 B、 C、 D、17. 如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( ) A、4:9 B、2:3 C、3:4 D、9:1618. 九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3,随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号,规定当两次摸出的小球标号相同时中奖,则中奖的概率为( )A、 B、 C、1 D、19.
A、4:9 B、2:3 C、3:4 D、9:1618. 九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3,随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号,规定当两次摸出的小球标号相同时中奖,则中奖的概率为( )A、 B、 C、1 D、19.如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
 A、1 B、2 C、3 D、620. 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
A、1 B、2 C、3 D、620. 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
21. 已知f(x)= ,则f(1)= = ,f(2)= = …若f(1)+f(2)+f(3)+…+f(n)= ,则n的值为 .22. 如图,正方形AOBC的两边在坐标轴上,D是OB的中点,直线CD的函数关系式为y=2x﹣6,则△CDE的面积为 . (平方单位)
 23. 从3,0,﹣1,﹣2,﹣3这五个数中,随机抽取一个数,作为函数y=(5﹣m2)x和关于x的方程(m+1)x2+mx+1=0中m的值,恰好使所得函数的图象经过第一、三象限,且方程有实数根的概率为 .24.
23. 从3,0,﹣1,﹣2,﹣3这五个数中,随机抽取一个数,作为函数y=(5﹣m2)x和关于x的方程(m+1)x2+mx+1=0中m的值,恰好使所得函数的图象经过第一、三象限,且方程有实数根的概率为 .24.如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2017次跳2017步就跳到了号位置上.

三、解答题
-
25. 烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:(1)、苹果进价为每千克多少元?(2)、乙超市获利多少元?并比较哪种销售方式更合算.26. 综合题。(1)、如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
 (2)、如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.
(2)、如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长. 27. 已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(1)、
27. 已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(1)、当点P与点Q重合时,如图1,写出QE与QF的数量关系,不证明;
 (2)、
(2)、当点P在线段AB上且不与点Q重合时,如图2,(1)的结论是否成立?并证明;
 (3)、
(3)、当点P在线段BA(或AB)的延长线上时,如图3,此时(1)的结论是否成立?请画出图形并给予证明.
 28.
28.如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
 (1)、求抛物线的解析式;(2)、抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)、
(1)、求抛物线的解析式;(2)、抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)、在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.
