2017年河北省唐山市迁安市中考数学一模试卷
试卷更新日期:2017-06-20 类型:中考模拟
一、选择题
-
1. 下列各数中,相反数为4的是( )A、4 B、﹣4 C、0.4 D、0.252. 下列计算正确的是( )A、2mn+3mn=6mn B、mn2+mn3=mn5 C、mn3÷mn2=n D、(mn3)2=m2n53. 如图,下列四组图形中的两个三角形是中心对称关系的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若分式 □ 运算结果为x,则在“□”中添加的运算符号为( )A、+ B、﹣ C、+或× D、﹣或÷5. 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
4. 若分式 □ 运算结果为x,则在“□”中添加的运算符号为( )A、+ B、﹣ C、+或× D、﹣或÷5. 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( ) A、100° B、120° C、140° D、160°6. 如图,反比例函数y= 的图象可能是( )A、
A、100° B、120° C、140° D、160°6. 如图,反比例函数y= 的图象可能是( )A、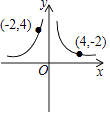 B、
B、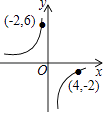 C、
C、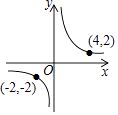 D、
D、 7. 下列几何体中,同一个几何体的主视图与俯视图不同的是( )A、
7. 下列几何体中,同一个几何体的主视图与俯视图不同的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知△ABC在正方形网格中的位置如图所示,则点P是△ABC的( )
8. 已知△ABC在正方形网格中的位置如图所示,则点P是△ABC的( )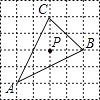 A、外心 B、内心 C、三条高线的交点 D、三条中线的交点9. 菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A、外心 B、内心 C、三条高线的交点 D、三条中线的交点9. 菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )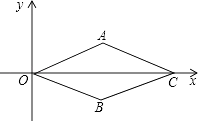 A、(3,1) B、(3,﹣1) C、(1,﹣3) D、(1,3)10. 有以下三种说法:①一组数据的平均数、中位数和众数都是唯一的 ②一组数据中最大值与最小值的平均数,就是这组数据的中位数 ③极差与方差都反映数据的波动,所以对于两组数据,极差大的一定方差大,方差大的一定极差大.其中,正确的说法有( )A、3个 B、2个 C、1个 D、0个11. 根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( )
A、(3,1) B、(3,﹣1) C、(1,﹣3) D、(1,3)10. 有以下三种说法:①一组数据的平均数、中位数和众数都是唯一的 ②一组数据中最大值与最小值的平均数,就是这组数据的中位数 ③极差与方差都反映数据的波动,所以对于两组数据,极差大的一定方差大,方差大的一定极差大.其中,正确的说法有( )A、3个 B、2个 C、1个 D、0个11. 根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( ) A、﹣1.7 B、﹣ C、﹣ D、﹣12. 小明在解决一个关于计算机病毒传播的问题时,设计算机有x台,列方程3+x+x(x+3)=48,则方程的解中一定不合题意的是( )A、5 B、9 C、﹣5 D、﹣913. 在▱ABCD中,∠ACB=25°,现将▱ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
A、﹣1.7 B、﹣ C、﹣ D、﹣12. 小明在解决一个关于计算机病毒传播的问题时,设计算机有x台,列方程3+x+x(x+3)=48,则方程的解中一定不合题意的是( )A、5 B、9 C、﹣5 D、﹣913. 在▱ABCD中,∠ACB=25°,现将▱ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( ) A、135° B、120° C、115° D、100°14. 关于x的方程 = 无解,则k的值为( )A、0或 B、﹣1 C、﹣2 D、﹣315. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A、135° B、120° C、115° D、100°14. 关于x的方程 = 无解,则k的值为( )A、0或 B、﹣1 C、﹣2 D、﹣315. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)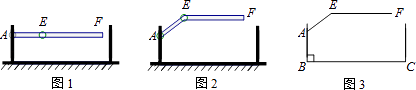 A、
A、 B、
B、 C、
C、 D、
D、 16. 如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ,CD= ,点P在四边形ABCD上,若P到BD的距离为 ,则点P的个数为( )
16. 如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ,CD= ,点P在四边形ABCD上,若P到BD的距离为 ,则点P的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
17. 的平方根是 .18. 若2x5y2m+3n与﹣3x3m+2ny6是同类项,则|m﹣n|= .19. 如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1 , 则∠A1=;∠A1BC与∠A1CD的平分线相交于点A2 , 得∠A2;…;∠An﹣1BC与∠An﹣1CD的平分线相交于点An , 要使∠An的度数为整数,则n的值最大为 .

三、解答题
-
20. 按照如下步骤计算:6﹣2÷( + ﹣ ﹣ ).(1)、计算:( + ﹣ ﹣ )÷6﹣2;(2)、根据两个算式的关系,直接写出6﹣2÷( + ﹣ ﹣ )的结果.21. 如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
 (1)、求证:∠A=∠BCD;(2)、点E运动多长时间,CF=AB?并说明理由.22. 在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.(1)、如果这个多边形是五边形,请求出这个外角的度数;(2)、是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.23. 小伟和小欣玩一种抽卡片游戏:将背面完全相同、正面分别写有1,2,3,4的四张卡片背面向上洗匀后,小伟和小欣各自随机抽取一张(不放回).将小伟的数字作为十位数字,小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否则小欣胜.(1)、当小伟抽取的卡片数字为2时,问两人谁获胜的可能性大?(2)、通过计算判断这个游戏对小伟和小欣是否公平.24. 小李创办了一家报刊零售点,对经营的某种晚报,他提供了如下信息:
(1)、求证:∠A=∠BCD;(2)、点E运动多长时间,CF=AB?并说明理由.22. 在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.(1)、如果这个多边形是五边形,请求出这个外角的度数;(2)、是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.23. 小伟和小欣玩一种抽卡片游戏:将背面完全相同、正面分别写有1,2,3,4的四张卡片背面向上洗匀后,小伟和小欣各自随机抽取一张(不放回).将小伟的数字作为十位数字,小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否则小欣胜.(1)、当小伟抽取的卡片数字为2时,问两人谁获胜的可能性大?(2)、通过计算判断这个游戏对小伟和小欣是否公平.24. 小李创办了一家报刊零售点,对经营的某种晚报,他提供了如下信息:①买进每份0.20元,卖出0.30元;
②在一个月内(以30天计),其中有20天每天可以卖出200份,其余的10天每天就只能卖出120份;
③一个月内,每天从报社买进的报纸份数必须相同,当天卖不掉的报纸以每份0.10元退回给报社.
(1)、第一个月为试营业阶段,他每天买进该晚报100份,这个月利润多少元?(2)、第二个月每天买进该晚报150份时,这个月利润多少元?(3)、设每天从报社买进晚报x份(120≤X≤200)时,月利润为y元,试写出y和x的函数关系式,并求出月利润的最大值.25. 如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔); (1)、如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,
(1)、如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,①则此时铁片是什么形状;
②给出证明,并通过计算说明此时铁片都能穿过圆孔;
 (2)、如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片;
(2)、如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片;
①当BE=DF= 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围.
26.如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
 (1)、求抛物线的函数表达式;(2)、求直线BC的函数表达式;(3)、点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
(1)、求抛物线的函数表达式;(2)、求直线BC的函数表达式;(3)、点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段PQ= AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.