2017年海南省定安县中考数学一模试卷
试卷更新日期：2017-06-20 类型：中考模拟
一、选择题
-
1. ﹣5的绝对值是（ ）A、5 B、 C、±5 D、﹣2. 下列计算正确的是（ ）A、2a5+a5=3a10 B、a2•a3=a6 C、（a2）3=a5 D、a10÷a2=a83. 当x=﹣1，y=2时，代数式x﹣y的值是（ ）A、1 B、﹣1 C、﹣3 D、24. 一组数据5，2，3，6，8，3的中位数和众数分别是（ ）A、4和3 B、4和8 C、3和3 D、5和35. 国家游泳中心﹣﹣“水立方”是北京2008年奥运会场馆之一，它的外层膜的展开面积约为260000平方米，将260000用科学记数法表示为2.6×10n ， 则n的值是（ ）A、3 B、4 C、5 D、66. 图是由5个大小相同的小正方体摆成的立体图形，它的俯视图是（ ）
A、
B、
C、
D、
7. 如图，已知AB∥CD，∠1=115°，∠2=65°，则∠C等于（ ）
A、40° B、45° C、50° D、60°8. 分式方程 ﹣ =0的解为（ ）A、x=1 B、x=2 C、x=3 D、x=49. 若反比例函数 的图象经过点（1，4），则它的图象也一定经过的点是（ ）A、（﹣1，﹣4） B、（1，﹣4） C、（4，﹣1） D、（﹣1，4）10. 在一个不透明的袋中装着2个红球和1个黄球，它们除颜色外其它均相同，随机从袋中摸出2个小球，两球恰好都是红球的概率为（ ）A、 B、 C、 D、11.如图，已知△ABC在平面直角坐标系中的位置如图所示，将△ABC先向下平移5个单位，再向左平移2个单位，则平移后C点的坐标是（ ）
A、（5，﹣2） B、（1，﹣2） C、（2，﹣1） D、（2，﹣2）12. 已知圆锥的母线长为5，底面半径为3，则圆锥的侧面积为（ ）A、15π B、24π C、30π D、39π13. 如图，在矩形ABCD中，E为AD的中点，∠BED的角平分线交BC于F．若AB=6，BC=16，则FC的长度为（ ）
A、4 B、5 C、6 D、814. 如图，⊙O是△ABC的外接圆，直径AD与BC相交于点E，连接CD，若⊙O的半径为5，AB=AC=8，则EC长为（ ）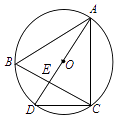
A、4 B、 C、 D、二、填空题
-
15. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC．若∠CAB=22.5°，CD=8cm，则⊙O的半径为 cm．
16. 分解因式：x2+6x+9= ．17. 龙眼的单价为a元/千克，香蕉的单价为b元/千克，买2千克龙眼和3千克香蕉共需元．18. 如图，在三角板ABC中，∠ACB=90°，∠A=30°，AC=6，将三角板ABC绕点C逆时针旋转，当起始位置时的点B恰好落在边A1B1上时，A1B的长为 ．
三、解答题
-
19. 计算(1)、 ×（﹣1）2﹣|﹣2|+（ ）﹣1；(2)、解不等式组： ．20. 某中学开展“阳光体育一小时”活动，按学校实际情况，决定开设A：踢毽子；B：篮球；C：跳绳；D：乒乓球四种运动项目．为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，并将调查结果绘制成如下两个统计图．请结合图中的信息解答下列问题：
(1)、本次共调查了名学生；(2)、在扇形统计图中，“B”所在扇形的圆心角是度；(3)、将条形统计图补充完整；(4)、若该中学有1200名学生，喜欢篮球运动的学生约有名．21. 受气候等因素的影响，今年某些农产品的价格有所上涨．张大叔在承包的10亩地里所种植的甲、乙两种蔬菜共获利13800元．其中甲种蔬菜每亩获利1200元，乙种蔬菜每亩获利1500元．则甲、乙两种蔬菜各种植了多少亩？22.如图，小敏在测量学校一幢教学楼AB的高度时，她先在点C测得教学楼的顶部A的仰角为30°，然后向教学楼前进12米到达点D，又测得点A的仰角为45°．请你根据这些数据，求出这幢教学楼AB的高度．
（结果精确到0.1米，参考数据： ≈1.73）
23. 如图，在正方形ABCD中，E是CD上一点，DF⊥BE交BE的延长线于点G，交BC的延长线于点F．
(1)、求证：△BCE≌△DCF．(2)、若∠DBE=∠CBE，求证：BD=BF．(3)、在（2）的条件下，求CE：ED的值．24.如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线y=﹣x2+bx+c经过A，B两点，点P在线段OA上，从点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以 个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．
(1)、求抛物线的解析式；(2)、当t为何值时，△APQ为直角三角形；(3)、过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标．