2017年广东省汕头市潮南区峡山街道中考数学模拟试卷(d卷)
试卷更新日期:2017-06-20 类型:中考模拟
一、选择题
-
1. 在﹣1,0,2, 四个数中,最大的数是( )A、﹣1 B、0 C、2 D、2. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
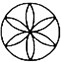 B、
B、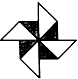 C、
C、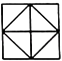 D、
D、 3. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
3. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )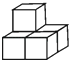 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 + = B、x6÷x3=x2 C、 =2 D、a2(﹣a2)=a45. 《世界保护益鸟公约》规定每年的4月1日为“国际爱鸟日”.因为有 它们,给我们的生活增添了靓丽的光彩.鸟类最昌盛的时期,约有160万种,用科学记数法可表示为( )A、1.6×105 B、1.6×106 C、1.6×107 D、1.6×1086. 一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时是绿灯的概率是( )
4. 下列计算正确的是( )A、 + = B、x6÷x3=x2 C、 =2 D、a2(﹣a2)=a45. 《世界保护益鸟公约》规定每年的4月1日为“国际爱鸟日”.因为有 它们,给我们的生活增添了靓丽的光彩.鸟类最昌盛的时期,约有160万种,用科学记数法可表示为( )A、1.6×105 B、1.6×106 C、1.6×107 D、1.6×1086. 一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时是绿灯的概率是( )
A、 B、 C、 D、7. 小玲每天骑自行车或步行上学,她上学的路程为2800米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为x米/分,根据题意,下面列出的方程正确的是( )A、 B、 C、 D、8. 某工厂分发年终奖金,具体金额和人数如下表所示,则下列对这组数据的说法中不正确的是( )人 数
1
3
5
70
10
8
3
金额(元)
200000
150000
80000
15000
10000
8000
5000
A、极差是195000 B、中位数是15000 C、众数是15000 D、平均数是150009. 关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是( )
A、m≤3 B、m<3 C、m<3且m≠2 D、m≤3且m≠210. 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
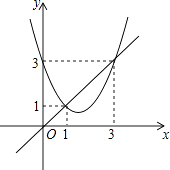 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
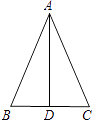
11. 分解因式:mn2+6mn+9m= .12. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC= .
 13. 如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO= .
13. 如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO= .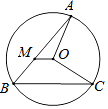 14. 如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是 .
14. 如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是 .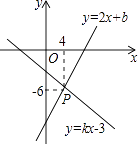 15. 观察下列等式
15. 观察下列等式12=1= ×1×2×(2+1)
12+22= ×2×3×(4+1)
12+22+32= ×3×4×(6+1)
12+22+32+42= ×4×5×(8+1)…
可以推测12+22+32+…+n2= .
三、解答题
-
16. 计算:( )﹣2﹣(π﹣ )0+| ﹣2|+4sin60°.17. 解不等式组: .18. 如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
四、解答题
-
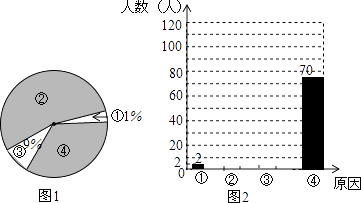
19. 中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”针对这种现象某媒体记者在多个路口采访闯红灯的行人,得出形成这种现象的四个基本原因,①红绿灯设置不科学,交通管理混乱占1%;②侥幸心态;③执法力度不够占9%;④从众心理,该记者将这次调查情况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题.(1)、该记者本次一共调査了名行人;(2)、求图1中④所在扇形的圆心角,并补全图2;
 (3)、在本次调查中,记者随机采访其中的一名行人,求他属于第②种情况的概率.20. 如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F
(3)、在本次调查中,记者随机采访其中的一名行人,求他属于第②种情况的概率.20. 如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F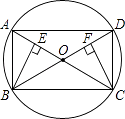 (1)、四边形ABCD是什么特殊的四边形?请判断并说明理由;(2)、求证:BE=CF.21. 目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: =1.41, =1.73)
(1)、四边形ABCD是什么特殊的四边形?请判断并说明理由;(2)、求证:BE=CF.21. 目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: =1.41, =1.73)
五、解答题
-
22. 如图,直线y=2x与反比例函数y= (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα= .
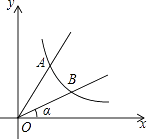 (1)、求k的值.(2)、求点B的坐标.(3)、设点P(m,0),使△PAB的面积为2,求m的值.23. 四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.(1)、利用图1,求证:四边形ABCD是菱形.
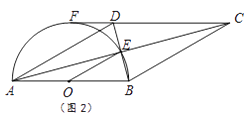
(1)、求k的值.(2)、求点B的坐标.(3)、设点P(m,0),使△PAB的面积为2,求m的值.23. 四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.(1)、利用图1,求证:四边形ABCD是菱形.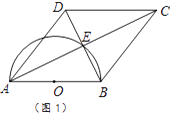 (2)、如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
(2)、如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.①连结OE,求△OBE的面积.
②求弧AE的长.
 24.
24.如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y= x+4,与x轴相交于点D.
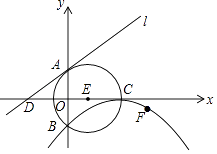 (1)、求抛物线的解析式;(2)、判断直线l与⊙E的位置关系,并说明理由;(3)、动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
(1)、求抛物线的解析式;(2)、判断直线l与⊙E的位置关系,并说明理由;(3)、动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.