2017年广东省东莞市中堂六校中考数学二模试卷

试卷更新日期：2017-06-20 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣5的绝对值是（）

A、 $\frac{1}{5}$ B、5 C、﹣ $\frac{1}{5}$ D、﹣5

查看试题解析
2. 科学家在实验中检测出某微生物细胞直径约为0.0000035米，将0.0000035用科学记数法表示为（）

A、3.5×1 0^﹣⁶ B、3.5×1 0⁶ C、3.5×1 0^﹣⁵ D、35×1 0^﹣⁵

查看试题解析
3. 下列计算中，正确的是（）

A、a•a²=a² B、（a+1）²=a²+1 C、（ab）²=ab² D、（﹣a）³=﹣a³

查看试题解析
4. 半径为6，圆心角为120°的扇形的面积是（）

A、3π B、6π C、9π D、12π

查看试题解析
5. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 把抛物线y=x²+4先向左平移1个单位，再向下平移3个单位，得到的抛物线的解析式为（）

A、y=（x+1）²+1 B、y=（x﹣1）²+1 C、y=（x﹣1）²+7 D、y=（x+1）²+7

查看试题解析
7. 如图，在平面直角坐标系中，点A的坐标为（4，3），那么cosα的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
8. a，b在数轴上的位置如图，化简|a+b|的结果是（）

A、﹣a﹣b B、a+b C、a﹣b D、b﹣a

查看试题解析
9. 如图，正方形AEFG的边AE放置在正方形ABCD的对角线AC上，EF与CD交于点M，得四边形AEMD，且两正方形的边长均为2，则两正方形重合部分（阴影部分）的面积为（）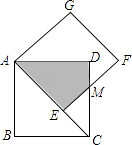

A、﹣4+4 $\sqrt{2}$ B、4 $\sqrt{2}$ +4 C、8﹣4 $\sqrt{2}$ D、 $\sqrt{2}$ +1

查看试题解析
10. 二次函数y=ax²+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：
①a＜0；②c＞0；③b²﹣4ac＞0；④ $\frac{a}{2 b}$ ＜0中，正确的结论有（）

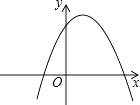A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解：x²y﹣y= ．

查看试题解析
12. 使 $\sqrt{x - 1}$ 有意义的x的取值范围是．

查看试题解析
13. 已知点P坐标为（1，1），将点P绕原点逆时针旋转45°得点P₁ ，则点P₁的坐标为．

查看试题解析
14. 若关于x的一元二次方程x²﹣2x+m=0有实数根，则m的取值范围是．

查看试题解析
15. 波音公司生产某种型号飞机，7月份的月产量为50台，由于改进了生产技术，计划9月份生产飞机98台，那么8、9月飞机生产量平均每月的增长率是．

查看试题解析
16.
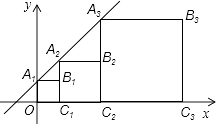
正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图所示的方式放置．点A₁ ， A₂ ， A₃ ， …和点C₁ ， C₂ ， C₃ ， …分别在直线y=kx+b（k＞0）和x轴上，已知点B₁（1，1），B₂（3，2），则B_n的坐标是．

查看试题解析

三、解答题

17. 计算：（ $\frac{1}{3}$ ）^﹣²﹣（﹣1）²⁰¹⁶﹣ $\sqrt{25}$ +（π﹣1）⁰ ．

查看试题解析
18. 先化简（1﹣ $\frac{3}{a + 2}$ ）÷ $\frac{a^{2} - 2 a + 1}{a^{2} - 4}$ ，然后从﹣ $\sqrt{5}$ ＜a $< \sqrt{5}$ 的范围内选取一个合适的整数作为a的值代入求值．

查看试题解析
19.
如图，在平行四边形ABCD中，

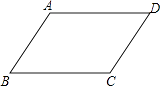(1)、以点A为圆心，AB长为半径画弧交AD于点F，再分别以B、F为圆心，大于 $\frac{1}{2}$ BF长为半径画弧，两弧交于一点P，连接AP并延长交BC于点E，连接EF；

(2)、四边形ABEF是（选填矩形、菱形、正方形、无法确定），说明理由．

查看试题解析

四、解答题

20. 有A、B两种饮料，这两种饮料的体积和单价如表：
类型
A
B
单瓶饮料体积/升
1
2.5
单价/元
3
4

(1)、小明购买A、B两种饮料共13升，用了25元，他购买A，B两种饮料个各多少瓶？

(2)、若购买A、B两种饮料共36瓶，且A种饮料的数量不多于B种饮料的数量，则最少可以购买多少升饮料？

查看试题解析
21. 某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象，已知探测线与地面的夹角分别是25°和60°，且AB=4米，求该生命迹象所在位置C的深度．（结果精确到1米．参考数据：sin25°≈0.4，cos25°≈0.9，tan25°≈0.5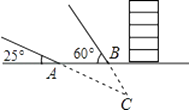， $\sqrt{3}$ ≈1.7）

查看试题解析
22.
某校要求八年级同学在课外活动中，必须在五项球类（篮球、足球、排球、羽毛球、乒乓球）活动中任选一项（只能选一项）参加训练，为了了解八年级学生参加球类活动的整体情况，现以八年级2班作为样本，对该班学生参加球类活动的情况进行统计，并绘制了如图所示的不完整统计表和扇形统计图：
八年级2班参加球类活动人数统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
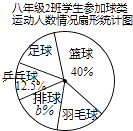
根据图中提供的信息，解答下列问题：

(1)、a= ， b=；

(2)、该校八年级学生共有600人，则该年级参加足球活动的人数约人；

(3)、该班参加乒乓球活动的5位同学中，有3位男同学（A，B，C）和2位女同学（D，E），现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成混合双打组合的概率．

查看试题解析

五、解答题

23. 如图，一次函数y=kx+b的图象与反比例函数y= $\frac{m}{x}$ （x＞0）的图象交于A（2，﹣1），B（ $\frac{1}{2}$ ，n）两点，直线y=2与y轴交于点C．

(1)、求一次函数与反比例函数的解析式；

(2)、求△ABC的面积．

查看试题解析
24. 如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．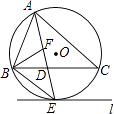

(1)、判断直线l与⊙O的位置关系，并说明理由；

(2)、若∠ABC的平分线BF交AD于点F，求证：BE=EF；

(3)、在（2）的条件下，若DE=4，DF=3，求AF的长．

查看试题解析
25.
如图（1）在Rt△ABC中，∠C=90°，AB=5cm．BC=a cm，AC=3cm，且a是方程x²﹣（m﹣1）x+m+4=0的根．

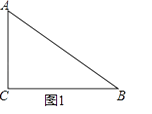(1)、求a和m的值；

(2)、
如图（2），有一个边长为 $\frac{a}{2}$ 的等边三角形DEF从C出发，以1cm/s的速度沿CB方向移动，至△DEF全部进入与△ABC为止，设移动时间为xs，△DEF与△ABC重叠部分面积为y，试求出y与x的函数关系式并注明x的取值范围；

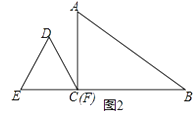(3)、试求出发后多久，点D在线段AB上？

查看试题解析

八年级2班参加球类活动人数统计表
项目	篮球	足球	乒乓球	排球	羽毛球
人数	a	6	5	7	6

类型	A	B
单瓶饮料体积/升	1	2.5
单价/元	3	4