2017年北京市石景山区中考数学一模试卷
试卷更新日期:2017-06-20 类型:中考模拟
一、选择题.
-
1.
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
 A、a B、b C、﹣b D、c2. 2016年9月15日天宫二号空间实验室在酒泉卫星发射中心发射成功,它的运行轨道距离地球393000米.将393000用科学记数法表示应为( )
A、a B、b C、﹣b D、c2. 2016年9月15日天宫二号空间实验室在酒泉卫星发射中心发射成功,它的运行轨道距离地球393000米.将393000用科学记数法表示应为( )
A、0.393×107 B、3.93×105 C、3.93×106 D、393×1033. 如图,直线a∥b,直线l与a,b分别交于A,B两点,过点B作BC⊥AB交直线a于点C,若∠1=65°,则∠2的度数为( ) A、25° B、35° C、65° D、115°4. 篆体是我国汉字古代书体之一.下列篆体字“美”,“丽”,“北”,“京”中,不是轴对称图形的为( )A、
A、25° B、35° C、65° D、115°4. 篆体是我国汉字古代书体之一.下列篆体字“美”,“丽”,“北”,“京”中,不是轴对称图形的为( )A、 B、
B、 C、
C、 D、
D、 5. 已知一个多边形的内角和等于这个多边形外角和的2倍,则这个多边形的边数是( )A、4 B、5 C、6 D、86. 在一个不透明的盒子中装有2个红球,3个黄球和4个白球,这些球除了颜色外无其他差别,现从这个盒子中随机摸出一个球,摸到红球的概率是( )A、 B、 C、 D、7. 若某几何体的三视图如图所示,则该几何体是( )
5. 已知一个多边形的内角和等于这个多边形外角和的2倍,则这个多边形的边数是( )A、4 B、5 C、6 D、86. 在一个不透明的盒子中装有2个红球,3个黄球和4个白球,这些球除了颜色外无其他差别,现从这个盒子中随机摸出一个球,摸到红球的概率是( )A、 B、 C、 D、7. 若某几何体的三视图如图所示,则该几何体是( )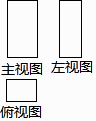 A、
A、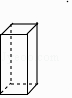 B、
B、 C、
C、 D、
D、 8. 周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( )
8. 周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( ) A、30千米/小时 B、18千米/小时 C、15千米/小时 D、9千米/小时9.
A、30千米/小时 B、18千米/小时 C、15千米/小时 D、9千米/小时9.用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于 DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
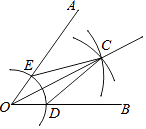 A、SAS B、ASA C、AAS D、SSS10. 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
A、SAS B、ASA C、AAS D、SSS10. 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( ) A、当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km B、消耗1升汽油,丙车最多可行驶5km C、当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同 D、当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少
A、当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km B、消耗1升汽油,丙车最多可行驶5km C、当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同 D、当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少二、填空题
-
11. 分解因式:2x2﹣18= .12. 请写出一个开口向下,并且过坐标原点的抛物线的表达式,y= .13. 为了测量校园里水平地面上的一棵大树的高度,数学综合实践活动小组的同学们开展如下活动:某一时刻,测得身高1.6m的小明在阳光下的影长是1.2m,在同一时刻测得这棵大树的影长是3.6m,则此树的高度是m.14. 如果x2+x﹣5=0,那么代数式(1+ )÷ 的值是 .15. 某雷达探测目标得到的结果如图所示,若记图中目标A的位置为(3,30°),目标B的位置为(2,180°),目标C的位置为(4,240°),则图中目标D的位置可记为 .
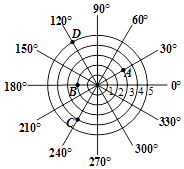 16. 首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012﹣2016年客流量统计结果如表:
16. 首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012﹣2016年客流量统计结果如表:年份
2012
2013
2014
2015
2016
客流量(万人次)
8192
8371
8613
8994
9400
根据统计表中提供的信息,预估首都国际机场2017年客流量约万人次,你的预估理由是 .
三、解答题
-
17. 计算:6sin60°﹣( )﹣2﹣ +|2﹣ |.18. 解不等式组: 并写出它的所有整数解.19. 如图,在四边形ABCD中,AB∥DC,E是CB的中点,AE的延长线与DC的延长线相交于点F.
求证:AB=FC.
 20. 列方程解应用题:
20. 列方程解应用题:我国元代数学家朱世杰所撰写的《算学启蒙》中有这样一道题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”
译文:良马平均每天能跑240里,驽马平均每天能跑150里.现驽马出发12天后良马从同一地点出发沿同一路线追它,问良马多少天能够追上驽马?
21. 关于x的一元二次方程mx2﹣(2m﹣3)x+(m﹣1)=0有两个实数根.(1)、求m的取值范围;(2)、若m为正整数,求此方程的根.22. 如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= (m≠0)交于点A(2,﹣3)和点B(n,2). (1)、求直线与双曲线的表达式;(2)、对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.23. 如图,在▱ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
(1)、求直线与双曲线的表达式;(2)、对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.23. 如图,在▱ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF. (1)、求证:四边形ABCD是菱形;(2)、若∠EAF=60°,CF=2,求AF的长.24. 阅读下列材料:2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上,环境问题再次成为大家议论的重点内容之一.
(1)、求证:四边形ABCD是菱形;(2)、若∠EAF=60°,CF=2,求AF的长.24. 阅读下列材料:2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上,环境问题再次成为大家议论的重点内容之一.北京自1984年开展大气监测,至2012年底,全市已建立监测站点35个.2013年,北京发布的首个PM2.5年均浓度值为89.5微克/立方米.2014年,北京空气中的二氧化硫年均浓度值达到了国家新的空气质量标准;二氧化氮、PM10、PM2.5年均浓度值超标,其中PM2.5年均浓度值为85.9微克/立方米.2016年,北京空气中的二氧化硫年均浓度值远优于国家标准;二氧化氮、PM10、PM2.5的年均浓度值分别为48微克/立方米、92微克/立方米、73微克/立方米.与2015年相比,二氧化硫、二氧化氮、PM10年均浓度值分别下降28.6%、4.0%、9.8%;PM2.5年均浓度值比2015年的年均浓度值80.6微克/立方米有较明显改善.(以上数据来源于北京市环保局)
根据以上材料解答下列问题:
(1)、2015年北京市二氧化氮年均浓度值为微克/立方米;(2)、请你用折线统计图将2013﹣2016年北京市PM2.5的年均浓度值表示出来,并在图上标明相应的数据.25. 如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上. (1)、求证:CD是⊙O的切线;(2)、点E是⊙O上一点,连接BE,CE.若∠BCE=42°,cos∠DAC= ,AC=m,写出求线段CE长的思路.26.
(1)、求证:CD是⊙O的切线;(2)、点E是⊙O上一点,连接BE,CE.若∠BCE=42°,cos∠DAC= ,AC=m,写出求线段CE长的思路.26.解答题
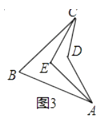
定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
 (1)、
(1)、性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
 (2)、
(2)、性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B=°.
 27. 在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+4a﹣3(a≠0)的顶点为A.
27. 在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+4a﹣3(a≠0)的顶点为A. (1)、求顶点A的坐标;(2)、过点(0,5)且平行于x轴的直线l,与抛物线y=ax2﹣4ax+4a﹣3(a≠0)交于B,C两点.
(1)、求顶点A的坐标;(2)、过点(0,5)且平行于x轴的直线l,与抛物线y=ax2﹣4ax+4a﹣3(a≠0)交于B,C两点.①当a=2时,求线段BC的长;
②当线段BC的长不小于6时,直接写出a的取值范围.
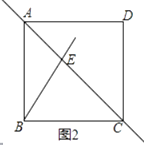
28. 在正方形ABCD中,点E是对角线AC上的动点(与点A,C不重合),连接BE.(1)、将射线BE绕点B顺时针旋转45°,交直线AC于点F.
①依题意补全图1;

②小研通过观察、实验,发现线段AE,FC,EF存在以下数量关系:
AE与FC的平方和等于EF的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
想法1:将线段BF绕点B逆时针旋转90°,得到线段BM,要证AE,FC,EF的关系,只需证AE,AM,EM的关系.
想法2:将△ABE沿BE翻折,得到△NBE,要证AE,FC,EF的关系,只需证EN,FN,EF的关系.
…
请你参考上面的想法,用等式表示线段AE,FC,EF的数量关系并证明;(一种方法即可)
(2)、如图2,若将直线BE绕点B顺时针旋转135°,交直线AC于点F.小研完成作图后,发现直线AC上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.
 29.
29.在平面直角坐标系xOy中,对“隔离直线”给出如下定义:
点P(x,m)是图形G1上的任意一点,点Q(x,n)是图形G2上的任意一点,若存在直线l:kx+b(k≠0)满足m≤kx+b且n≥kx+b,则称直线l:y=kx+b(k≠0)是图形G1与G2的“隔离直线”.
如图1,直线l:y=﹣x﹣4是函数y= (x<0)的图象与正方形OABC的一条“隔离直线”.
 (1)、在直线y1=﹣2x,y2=3x+1,y3=﹣x+3中,是图1函数y= (x<0)的图象与正方形OABC的“隔离直线”的为;
(1)、在直线y1=﹣2x,y2=3x+1,y3=﹣x+3中,是图1函数y= (x<0)的图象与正方形OABC的“隔离直线”的为;请你再写出一条符合题意的不同的“隔离直线”的表达式:;
(2)、如图2,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标是( ,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
 (3)、
(3)、正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点M(1,t)是此正方形的中心.若存在直线y=2x+b是函数y=x2﹣2x﹣3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,请直接写出t的取值范围.
