2016-2017学年江西省宜春市八年级上学期期末数学试卷
试卷更新日期：2017-06-20 类型：期末考试
一、选择题
-
1. 一粒米的质量是0.000025千克，将0.000025用科学记数法表示为（ ）A、0.25×10﹣4 B、2.5×10﹣5 C、2.5×10﹣4 D、25×10﹣62. 若多项式x2+ax+b分解因式的结果（x﹣2）（x+3），则a，b的值分别是（ ）A、a=1，b=﹣6 B、a=5，b=6 C、a=1，b=6 D、a=5，b=﹣63. 已知等腰三角形一边长为4，一边的长为6，则等腰三角形的周长为（ ）A、14 B、16 C、10 D、14或164. 如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于，且OD=4，△ABC的面积是（ ）
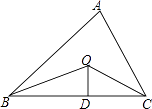A、25 B、84 C、42 D、215. 化简 ﹣（a+1）的结果是（ ）A、 B、 C、 D、6. 如图，△ABC沿直线L对折后能与△ADC重合，且AB∥CD，下列选项正确的是（ ）
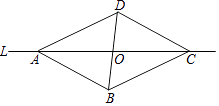A、AB=CD，AO=OC B、AB=BD，∠BAD=∠DCB C、AB∥BC，BC=BD D、OD=OB，∠CDB=∠BCD二、填空题
-
7. 分解因式：x3﹣9x= ．8. 若9x2+kx+1是一个完全平方式，则k= ．9.
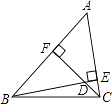
如图，已知BE和CF是△ABC的两条高，∠ABC=48°，∠ACB=76°，则∠FDE= ．
10. 如图，Rt△ABC中，∠BAC=90°，AB=AC，BD⊥直线L于D，CE⊥直线L于E，若BD=5cm，CE=4cm，则DE= ．
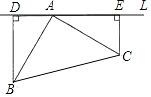11. 若am=2，an=3，则a3m+2n= ．12. 如图，∠AOB=60°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为 ．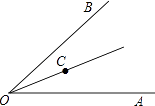
三、解答题。
-
13. 先化简，再求值：2a（a+2b）﹣（a+2b）2 ， 其中=1，b=﹣2．14. 若一个多边形的每一个内角都等于120°，求该多边形的边数．15. 解分式方程： ﹣1= ．16. 如图，已知F是DE的中点，∠D=∠E，∠DFN=∠EFM．求证：DM=EN．
17. 已知：如图，AB比AC长2cm，BC的垂直平分线交AB于点D，交BC于点E，△ACD的周长是14cm，求AB和AC的长．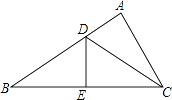
18. 如图，在平面直角坐标系中，A（﹣3，2），B（﹣4，﹣3），C（﹣1，﹣1）．
(1)、在图中作出△ABC关于y轴对称的△A1B1C1；(2)、写出点△A1 ， B1 ， C1的坐标（直接写答案）：A1；B1；C1；(3)、△A1B1C1的面积为；(4)、在y轴上画出点P，使PB+PC最小．19. 如图，AC平分∠BCD，AB=AD，AE⊥BC于E，AF⊥CD于F．
(1)、若∠ABE=60°，求∠CDA的度数．(2)、若AE=2，BE=1，CD=4．求四边形AECD的面积．20. 如图，AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．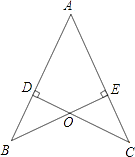
(1)、求证：AD=AE；(2)、连接OA，BC，试判断直线OA，BC的关系并说明理由．21. 有160个零件，平均分配给甲、乙两个车间加工，乙车间因另有紧急任务，所以在甲车间加工3小时后才开始加工，因此比甲车间迟20分钟完成。(1)、已知甲、乙两车间的生产效率的比是1：3，则甲、乙两车间每小时各能加工多少零件？(2)、如果零件总数为a个，（1）中其它条件不变，则甲、乙两车间每小时各加工多少个零件（用含a的式子表示）．22. 综合题。(1)、问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
①∠AEB的度数为
②猜想线段AD，BE之间的数量关系为： ， 并证明你的猜想．
(2)、拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM 为△DCE中DE边上的高，连接BE，请求出∠AEB的度数及线段CM，AE，BE 之间的数量关系．
