云南省陆良县2019届高三文数第二次适应性考试试卷
试卷更新日期:2019-08-13 类型:高考模拟
一、单选题
-
1. 设集合 ,则 ( )A、 B、 C、 D、2. 已知复数 满足 ,则 ( )A、 B、 C、 D、3. 已知命题 ,那么 是( )A、 B、 C、 D、4. 图1是某学习小组学生数学考试成绩的茎叶图,1号到16号的同学的成绩依次为 ,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )

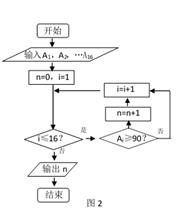 A、6 B、7 C、10 D、165. 已知 ,且 ,则 ( )A、 B、 C、 D、6. 设 ,则 的大小关系为( )A、 B、 C、 D、7. 设函数 的最小正周期为 ,且 ,则 ( )A、 在 上单调递减 B、 在 上单调递减 C、 在 上单调递增 D、 在 上单调递增8. 已知双曲线 的左右焦点为 ,过左焦点 作垂直于 轴的直线交 双曲线的两条渐近线于 两点,若 是直角,则双曲线的离心率是( ).A、 B、 C、 D、9. 已知正方体 的棱长为1, 是棱 的中点,点 在正方体内部或正方体的表面上,且 平面 ,则动点 的轨迹所形成的区域面积是( )A、 B、 C、 D、10. 已知三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( )
A、6 B、7 C、10 D、165. 已知 ,且 ,则 ( )A、 B、 C、 D、6. 设 ,则 的大小关系为( )A、 B、 C、 D、7. 设函数 的最小正周期为 ,且 ,则 ( )A、 在 上单调递减 B、 在 上单调递减 C、 在 上单调递增 D、 在 上单调递增8. 已知双曲线 的左右焦点为 ,过左焦点 作垂直于 轴的直线交 双曲线的两条渐近线于 两点,若 是直角,则双曲线的离心率是( ).A、 B、 C、 D、9. 已知正方体 的棱长为1, 是棱 的中点,点 在正方体内部或正方体的表面上,且 平面 ,则动点 的轨迹所形成的区域面积是( )A、 B、 C、 D、10. 已知三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( ) A、 B、 C、 D、11. 已知点 ,过抛物线 上一点 的直线与直线 垂直相交于点 ,若 ,则 的横坐标为( )A、 B、2 C、 D、112. 已知关于 的方程 有2个不相等的实数根,则 的取值范围是( ).A、 B、 C、 D、
A、 B、 C、 D、11. 已知点 ,过抛物线 上一点 的直线与直线 垂直相交于点 ,若 ,则 的横坐标为( )A、 B、2 C、 D、112. 已知关于 的方程 有2个不相等的实数根,则 的取值范围是( ).A、 B、 C、 D、二、填空题
-
13. 已知向量 , ,若 ,则 的值为14. 如图,点 是 的边 上一点, , , , , 。
 15. 若点 (其中 )为平面区域 内的一个动点,已知点 , 为坐标原点,则 的最小值为 。16. 已知函数 在区间 上单调递减,在 上单调递增,则实数 的取值范围是 .
15. 若点 (其中 )为平面区域 内的一个动点,已知点 , 为坐标原点,则 的最小值为 。16. 已知函数 在区间 上单调递减,在 上单调递增,则实数 的取值范围是 .三、解答题
-
17. 已知数列 的前n项和 满足 ,其中 .
(Ⅰ)证明:数列 为等比数列;
(Ⅱ)设 ,求数列 的前n项和 .
18. 某中学有初中学生1800人,高中学生1200人. 为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组: , , , , ,并分别加以统计,得到如图所示的频率分布直方图.

(Ⅰ)写出 的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(Ⅱ)从阅读时间不足10个小时的样本学生中随机抽取2人,求至少抽到1名高中生的概率.
19. 如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.
(Ⅰ)求证:OM∥平面PAB;
(Ⅱ)平面PBD⊥平面PAC;
(Ⅲ)当三棱锥C﹣PBD的体积等于 时,求PA的长.
20. 已知椭圆C 的离心率为 ,点 在椭圆C上.直线l过点(1,1),且与椭圆C交于A,B两点,线段AB的中点为M.(I)求椭圆C的方程;
(Ⅱ)点O为坐标原点,延长线段OM与椭圆C交于点P,四边形OAPB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.