2017年浙江省绍兴市中考数学试卷
试卷更新日期:2017-06-20 类型:中考真卷
一、选择题
-
1. -5的相反数是( )A、 B、5 C、 D、-52. 研究表明,可燃冰是一种可替代石油的新型清洁能源。在我国某海域已探明的可燃冰储存量达150 000 000 000立方米,其中数字150 000 000 000用科学记数法可表示为( )
A、15×1010 B、0.15×1012 C、1.5×1011 D、1.5×10123.如图的几何体由五个相同的小正方体搭成,它的主视图是( )
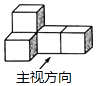 A、
A、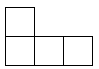 B、
B、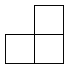 C、
C、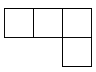 D、
D、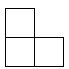 4. 在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其它均相同,从中任意摸出一个球,则摸出黑球的概率是( )
4. 在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其它均相同,从中任意摸出一个球,则摸出黑球的概率是( )
A、 B、 C、 D、5. 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:甲
乙
丙
丁
平均数(环)
9.14
9.15
9.14
9.15
方差
6.6
6.8
6.7
6.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 ( )
A、甲 B、乙 C、丙 D、丁6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为( )
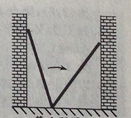 A、0.7米 B、1.5米 C、2.2米 D、2.4米7.
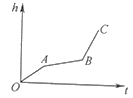
A、0.7米 B、1.5米 C、2.2米 D、2.4米7.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
 A、
A、 B、
B、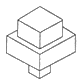 C、
C、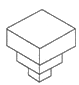 D、
D、 8.
8.在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。若∠ACB=21°,则∠ECD的度数是( )
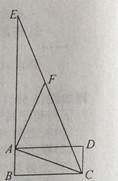 A、7° B、21° C、23° D、24°9. 矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A、7° B、21° C、23° D、24°9. 矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
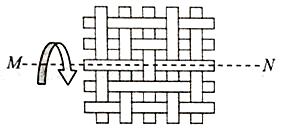
A、y=x2+8x+14 B、y=x2-8x+14 C、y=x2+4x+3 D、y=x2-4x+310.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
 A、
A、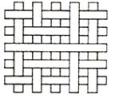 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 分解因式: =.12.
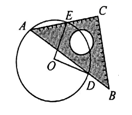
如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E.则∠DOE的度数为.
 13.
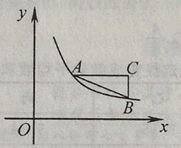
13.如图,Rt△ABC的两个锐角顶点A,B在函数y= (x>0)的图象上,AC//x轴,AC=2.若点A的坐标为(2,2),则点B的坐标为.
 14.
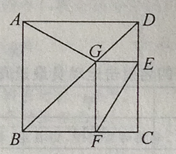
14.如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.
 15. 以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB的长为.
15. 以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB的长为.
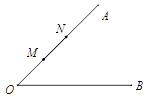
16.如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.
三、解答题
-
17. 计算题。(1)、计算: .(2)、解不等式:4x+5≤2(x+1).18.
某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
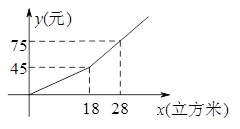 (1)、若某月用水量为18立方米,则应交水费多少元?(2)、求当x>18时,y关于x的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?19.
(1)、若某月用水量为18立方米,则应交水费多少元?(2)、求当x>18时,y关于x的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?19.为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如下图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题.
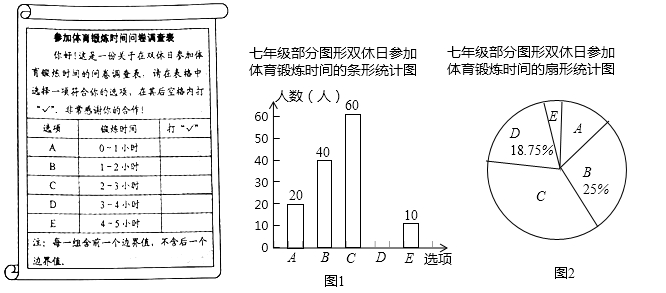 (1)、本次接受问卷调查的同学有多少人?补全条形统计图.(2)、本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.20.
(1)、本次接受问卷调查的同学有多少人?补全条形统计图.(2)、本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.20.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶中D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)
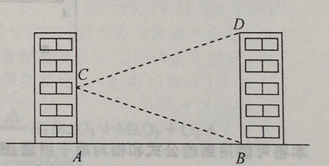 (1)、求∠BCD的度数.(2)、求教学楼的高BD21.
(1)、求∠BCD的度数.(2)、求教学楼的高BD21.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).

 (1)、如图1,问饲养室长x为多少时,占地面积y最大?(2)、如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.”小敏的说法正确吗?
(1)、如图1,问饲养室长x为多少时,占地面积y最大?(2)、如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.”小敏的说法正确吗?
22.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
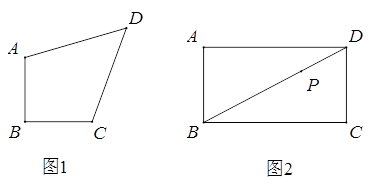 (1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
(1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)、如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.23.已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
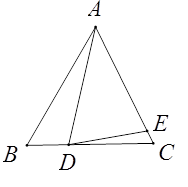 (1)、如图,若点D在线段BC上,点E在线段AC上.
(1)、如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)、是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.24.如图1,已知▱ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是▱ABCD边上的一个动点.

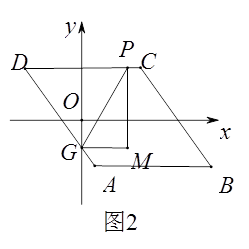 (1)、若点P在边BC上,PD=CD,求点P的坐标.(2)、若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)、若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
(1)、若点P在边BC上,PD=CD,求点P的坐标.(2)、若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)、若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).