2017年北京市丰台区中考数学一模试卷

试卷更新日期：2017-06-19 类型：中考模拟

进入出卷网下载

一、选择题．

1. 随着“一带一路”的建设推进，北京丰台口岸进口货值业务量加速增长，2016年北京丰台口岸进口货值飙升至189 000 000美元，比上一年翻了三倍，创下历史新高．将189 000 000用科学记数法表示应为（）

A、189×10⁶ B、1.89×10⁶ C、18.9×10⁷ D、1.89×10⁸

查看试题解析
2. 实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（）

A、|a|＞b B、|b|＜a C、﹣a＜a D、﹣b＜a

查看试题解析
3. 北京教育资源丰富，高校林立，下面四个高校校徽主体图案是中心对称图形的是（）

A、北京林业大学 B、北京体育大学 C、北京大学 D、中国人民大学

查看试题解析
4. 如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n的最小值为（）

A、45 B、60 C、72 D、144

查看试题解析
5.
在与国际友好学校交流活动中，小敏打算制做一个正方体礼盒送给外国朋友，每个面上分别书写一种中华传统美德，一共有“仁义礼智信孝”六个字．如图是她设计的礼盒平面展开图，那么“礼”字对面的字是（）

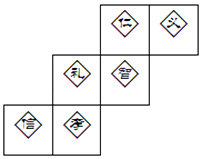A、义 B、仁 C、智 D、信

查看试题解析
6. 如果m²+2m﹣2=0，那么代数式（m+ $\frac{4 m + 4}{m}$ ）• $\frac{m^{2}}{m + 2}$ 的值是（）

A、﹣2 B、﹣1 C、2 D、3

查看试题解析
7. 如图，比例规是一种画图工具，它由长度相等的两脚AC和BD交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC，OB=3OD），然后张开两脚，使A，B两个尖端分别在线段a的两个端点上，当CD=1.8cm时，则AB的长为（）

A、7.2 cm B、5.4 cm C、3.6 cm D、0.6 cm

查看试题解析
8. 如图，这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图，如果他家去年总开支为6万元，那么用于教育的支出为（）

A、3万元 B、 $\frac{5}{3}$ 万元 C、2.4万元 D、2万元

查看试题解析
9. 如图在正方形网格中，若A（1，1），B（2，0），则C点的坐标为（）

A、（﹣3，﹣2） B、（3，﹣2） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
10.
近年来由于空气质量的变化，以及人们对自身健康的关注程度不断提高，空气净化器成为很多家庭的新电器．某品牌的空气净化器厂家为进一步了解市场，制定生产计划，根据2016年下半年销售情况绘制了如下统计图，其中同比增长率=（ $\frac{当月销售量}{去年同月销售量}$ ﹣1）×100%，下面有四个推断：
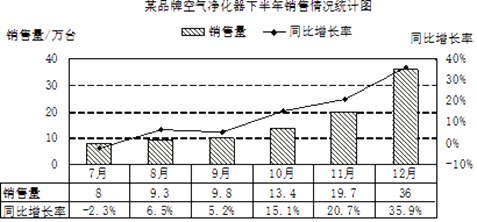
①2016年下半年各月销售量均比2015年同月销售量增多
②第四季度销售量占下半年销售量的七成以上
③下半年月均销售量约为16万台
④下半年月销售量的中位数不超过10万台
其中合理的是（）

A、①② B、①④ C、②③ D、③④

查看试题解析

二、填空题

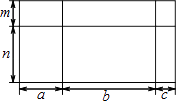
11. 如果二次根式 $\sqrt{x + 4}$ 有意义，那么x的取值范围是．

查看试题解析
12. 图中的四边形均为矩形，根据图形的面积关系，写出一个正确的等式：．

查看试题解析
13. 一天上午林老师来到某中学参加该校的校园开放日活动，他打算随机听一节九年级的课程，下表是他拿到的当天上午九年级的课表，如果每一个班级的每一节课被听的可能性是一样的，那么听数学课的可能性是．
班级
节次
1班
2班
3班
4班
第1节
语文
数学
外语
化学
第2节
数学
政治
物理
语文
第3节
物理
化学
体育
数学
第4节
外语
语文
政治
体育

查看试题解析
14. 如图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P在大量角器上对应的度数为40°，那么在小量角器上对应的度数为．（只考虑小于90°的角度）

查看试题解析
15. 众所周知，中华诗词博大精深，集大量的情景情感于短短数十字之间，或豪放，或婉约，或思民生疾苦，或抒发己身豪情逸致，文化价值极高．而数学与古诗词更是有着密切的联系．古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗，每句都是七个字．有一本诗集，其中五言绝句比七言绝句多13首，总字数却反而少了20个字．问两种诗各多少首？设七言绝句有x首，根据题意，可列方程为．

查看试题解析
16.
在数学课上，老师提出如下问题：已知：线段a，b（如图1）．
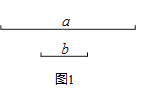
求作：等腰△ABC，使AB=AC，BC=a，BC边上的高为b．
小姗的作法如下：如图2，
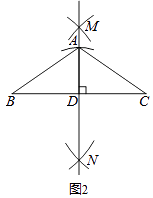
（i）作线段BC=a；
（ii）作线段BC的垂直平分线MN交线段BC于点D；
（iii）在MN上截取线段DA=b，连接AB，AC．所以，△ABC就是所求作的等腰三角形．
老师说：“小姗的作法正确”．
请回答：得到△ABC是等腰三角形的依据是：．

查看试题解析

三、解答题

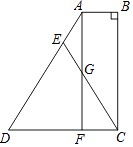
17. 计算： $\sqrt{12}$ ﹣（4﹣π）⁰+cos60°﹣| $\sqrt{3}$ ﹣3|．

查看试题解析
18. 解不等式组： ${\begin{matrix} 2 (x - 6) > x - 10 \\ x - 1 \leq \frac{5 x - 9}{3} \end{matrix}$ ．

查看试题解析
19. 如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且AB=FC，E为AD上一点，EC交AF于点G，EA=EG．
求证：ED=EC．

查看试题解析
20. 已知关于x的一元二次方程3x²﹣kx+k﹣4=0．

(1)、判断方程根的情况；

(2)、若此方程有一个整数根，请选择一个合适的k值，并求出此时方程的根．

查看试题解析
21. 如图，在平面直角坐标系xOy中，直线y=﹣3x+m与双曲线y= $\frac{k}{x}$ 相交于点A（m，2）．

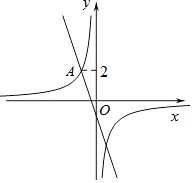(1)、求双曲线y= $\frac{k}{x}$ 的表达式；

(2)、过动点P（n，0）且垂直于x轴的直线与直线y=﹣3x+m及双曲线y= $\frac{k}{x}$ 的交点分别为B和C，当点B位于点C下方时，求出n的取值范围．

查看试题解析
22. 课题学习：设计概率模拟实验．
在学习概率时，老师说：“掷一枚质地均匀的硬币，大量重复实验后，正面朝上的概率约是 $\frac{1}{2}$ ．”小海、小东、小英分别设计了下列三个模拟实验：
小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷，然后计算瓶盖口朝上的次数与总次数的比值；
小东用硬纸片做了一个圆形转盘，转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字（如图2），转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值；
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3），其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验，然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．
根据以上材料回答问题：
小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处．

查看试题解析
23. 如图，在四边形ABCD中，∠ABC=90°，DE⊥AC于点E，且AE=CE，DE=5，EB=12．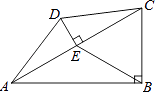

(1)、求AD的长；

(2)、若∠CAB=30°，求四边形ABCD的周长．

查看试题解析
24. 阅读下列材料：
由于发展时间早、发展速度快，经过20多年大规模的高速开发建设，北京四环内，甚至五环内可供开发建设的土地资源越来越稀缺，更多的土地供应将集中在五环外，甚至六环外的远郊区县．
据中国经济网2017年2月报道，来自某市场研究院的最新统计，2016年，剔除了保障房后，在北京新建商品住宅交易量整体上涨之时，北京各区域的新建商品住宅交易量则是有涨有跌．其中，昌平、通州、海淀、朝阳、西城、东城六区下跌，跌幅最大的为朝阳区，新建商品住宅成交量比2015年下降了46.82%．而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨，涨幅最大的为顺义区，比2015年上涨了118.80%．另外，从环线成交量的占比数据上，同样可以看出成交日趋郊区化的趋势．根据统计，2008年到2016年，北京全市成交的新建商品住宅中，二环以内的占比逐步从3.0%下降到了0.2%；二、三环之间的占比从5.7%下降到了0.8%；三、四环之间的占比从12.3%下降到了2.3%；四、五环之间的占比从21.9%下降到了4.4%．也就是说，整体成交中位于五环之内的新房占比，从2008年的42.8%下降到了2016年的7.7%，下滑趋势非常明显．由此可见，新房市场的远郊化是北京房地产市场发展的大势所趋．（注：占比，指在总数中所占的比重，常用百分比表示）
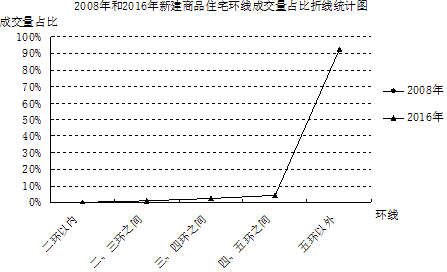
根据以上材料解答下列问题：

(1)、补全折线统计图；

(2)、根据材料提供的信息，预估 2017年位于北京市五环之内新建商品住宅成交量占比约，你的预估理由是．

查看试题解析
25. 如图，AB是⊙O的直径，C，D为⊙O上两点，CF⊥AB于点F，CE⊥AD交AD的延长线于点E，且CE=CF．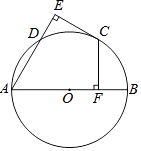

(1)、求证：CE是⊙O的切线；

(2)、连接CD，CB．若AD=CD=a，写出求四边形ABCD面积的思路．

查看试题解析
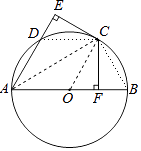26. 【问题情境】
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长
最小？最小值是多少？
【数学模型】
设该矩形的长为x，周长为y，则y与x的函数表达式为y=2（x+ $\frac{a}{x}$ ）（x＞0）．
【探索研究】
小彬借鉴以前研究函数的经验，先探索函数y=x+ $\frac{1}{x}$ 的图象性质．

(1)、结合问题情境，函数y=x+ $\frac{1}{x}$ 的自变量x的取值范围是x＞0，如表是y与x的几组对应值．
x
…
   $\frac{1}{4}$
   $\frac{1}{3}$
   $\frac{1}{2}$
1
2
3
m
…
y
…
4 $\frac{1}{4}$
3 $\frac{1}{3}$
2 $\frac{1}{2}$
2
2 $\frac{1}{2}$
3 $\frac{1}{3}$
4 $\frac{1}{4}$
…
①写出m的值；
②画出该函数图象，结合图象，得出当x=时，y有最小值，y_最小=；

(2)、【解决问题】
直接写出“问题情境”中问题的结论．

查看试题解析
27. 在平面直角坐标系xOy中，抛物线y=mx²﹣4mx+2m﹣1（m≠0）与平行于x轴的一条直线交于A，B两点．

(1)、求抛物线的对称轴；

(2)、如果点A的坐标是（﹣1，﹣2），求点B的坐标；

(3)、抛物线的对称轴交直线AB于点C，如果直线AB与y轴交点的纵坐标为﹣1，且抛物线顶点D到点C的距离大于2，求m的取值范围．

查看试题解析
28.
在边长为5的正方形ABCD中，点E，F分别是BC，DC边上的两个动点（不与点B，C，D重合），且AE⊥EF．

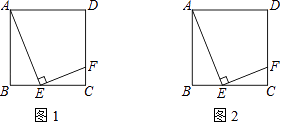(1)、如图1，当BE=2时，求FC的长；

(2)、延长EF交正方形ABCD外角平分线CP于点P．

①依题意将图2补全；
②小京通过观察、实验提出猜想：在点E运动的过程中，始终有AE=PE．小京把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的三种想法：
想法1：在AB上截取AG=EC，连接EG，要证AE=PE，需证△AGE≌△ECP．
想法2：作点A关于BC的对称点H，连接BH，CH，EH．要证AE=PE，需证△EHP为等腰三角形．
想法3：将线段BE绕点B顺时针旋转90°，得到线段BM，连接CM，EM，要证AE=PE，需证四边形MCPE为平行四边形．
请你参考上面的想法，帮助小京证明AE=PE．（一种方法即可）

查看试题解析
29. 在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：
如果矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形．点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形．例如，下图中的矩形A₁B₁C₁D₁ ， A₂B₂C₂D₂ ， AB₃C₃D₃都是点A，B，C的覆盖矩形，其中矩形AB₃C₃D₃是点A，B，C的最优覆盖矩形．

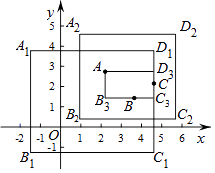(1)、已知A（﹣2，3），B（5，0），C（t，﹣2）．
①当t=2时，点A，B，C的最优覆盖矩形的面积为；
②若点A，B，C的最优覆盖矩形的面积为40，求直线AC的表达式；

(2)、已知点D（1，1）．E（m，n）是函数y= $\frac{4}{x}$ （x＞0）的图象上一点，⊙P是点O，D，E的一个面积最小的最优覆盖矩形的外接圆，求出⊙P的半径r的取值范围．

查看试题解析

班级节次	1班	2班	3班	4班
第1节	语文	数学	外语	化学
第2节	数学	政治	物理	语文
第3节	物理	化学	体育	数学
第4节	外语	语文	政治	体育

x	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	m	…
y	…	4 $\frac{1}{4}$	3 $\frac{1}{3}$	2 $\frac{1}{2}$	2	2 $\frac{1}{2}$	3 $\frac{1}{3}$	4 $\frac{1}{4}$	…