2017年安徽省阜阳市太和县中考数学一模试卷

试卷更新日期：2017-06-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数，如果盈利50元记作+50元，那么亏本30元记作：（）

A、﹣30元 B、﹣50元 C、+50元 D、+30元

查看试题解析
2. 下列运算正确的是：（）

A、（a﹣b）²=a²﹣b² B、a¹⁰÷a²=a⁵ C、（2a²b³）³=8a⁶b⁹ D、2a²•3a³=6a⁶

查看试题解析
3. 安徽省，政府工作报告》指出，2017年全年将实施亿元以上技改项目1000项，完成投资6600亿元，把6600亿用科学记数法可表示为（）

A、6.6×10³ B、66×10¹⁰ C、6.600×10¹¹ D、0.66×10¹²

查看试题解析
4. 三本相同的书本叠成如图所示的几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列二次根式中，与 $\sqrt{2}$ 之积为有理数的是（）

A、 $\sqrt{18}$ B、 $\sqrt{\frac{3}{4}}$ C、 $\sqrt{12}$ D、﹣ $\sqrt{27}$

查看试题解析
6. ）若|x+y﹣5|与（x﹣y﹣1）²互为相反数，则x²﹣y²的值为（）

A、﹣5 B、5 C、13 D、15

查看试题解析
7. 如表是某毕业班理化实验测试的分数分布，对于不同的x，下列关于分数的统计量不会发生改变的是（）
分数/分
7
8
9
10
频数
2
9﹣x
x+14
24

A、众数、方差 B、中位数、方差 C、众数、中位数 D、平均数、中位数

查看试题解析
8. AD是△ABC的高，AC=2 $\sqrt{5}$ ，AD=4，把△ADC沿着直线AD对折，点C落在点E的位置，如果△ABE是等腰三角形，那么线段BE的长度为（）

A、2 $\sqrt{5}$ B、2 $\sqrt{5}$ 或5 C、2 $\sqrt{6}$ D、5

查看试题解析
9. 甲、乙两车从A地出发沿同一路线驶向B地，甲车匀速驶向B地，甲车出发30分钟后，乙车才出发，乙先匀速行驶一段时间后，到达货站装货后继续行驶，速度减少了56千米/时，结果与甲车同时到达B地，甲乙两车距A地的路程y（千米）与乙车行驶时间x（时）之间的函数图象如图所示，下列说法中正确的是（）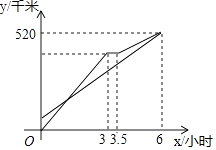

A、甲车从A地到B地行驶了6小时 B、甲的速度是120千米/时 C、乙出发90分钟追上甲 D、当两车在行驶过程中，相距40千米时，x=2或3.5

查看试题解析
10.
如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（）

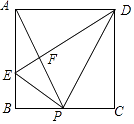A、当P为BC中点，△APD是等边三角形 B、当△ADE∽△BPE时，P为BC中点 C、当AE=2BE时，AP⊥DE D、当△APD是等边三角形时，BE+CD=DE

查看试题解析

二、填空题

11. 计算：4cos60°﹣ $\sqrt[3]{8}$ +（3﹣π）⁰= ．

查看试题解析
12. 随着各地对房地产市场调控的深入，近来某市房价持续回落，某楼盘原价为每平方米12000元，第一次降价后，销售业绩没有预期回升，于是再次降价，比第一次多降了10%，两次降价后售价为每平方米8640元，设第一次降价百分率为x，则可列方程为：．

查看试题解析
13. 分式方程 $\frac{6}{x^{2} - 9}$ ﹣1= $\frac{x}{3 - x}$ 的解是x= ．

查看试题解析
14. 如图，D为△ABC中边BC中点，E为CD上一点，将△ACE沿AE折叠时C与D重合，F为AB上一点，FB=FC，FC与AD、AE分别交于P、Q点，下列结论
①AE∥DF；②△APQ≌△DPF；
③AF=DF；④ $\frac{A F}{C P} = \frac{2}{3}$ ．
其中正确的有．

查看试题解析

三、解答题

15. 求不等式组 ${\begin{matrix} 3 x + 3 > 5 (x - 1) ① \\ \frac{2 x - 2}{3} - 1 \leq \frac{3 x}{2} ② \end{matrix}$ 的解集，并把它们的解集在数轴上表示出来．

查看试题解析
16. 从2开始，连续的偶数相加，它们和的情况如表：
加数的个数n
S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=15=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6

(1)、根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=；

(2)、
如下数表是由从1开始的连续自然数组成，观察规律：
①第n行的第一个数可用含n的式子表示为；

查看试题解析

四、解答题

17.
如图，方格中，每个小正方形的边长都是单位1，△ABC在平面直角坐标系中的位置如图．

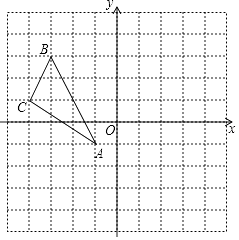(1)、①画出△ABC关于y轴对称的△A₁B₁C₁；
②画出△ABC绕点O按顺时针方向旋转90°后的△A₂B₂C₂；

(2)、判断△A₁B₁C₁和△A₂B₂C₂是不是成轴对称？如果是，请在图中作出它们的对称轴．

查看试题解析
18.
如图，四边形ABCD是某新建厂区示意图，∠A=75°，∠B=45°，BC⊥CD，AB=500 $\sqrt{2}$ 米，AD=200米，现在要在厂区四周建围墙，求围墙的长度有多少米？

查看试题解析
19. 某校组织学生参观航天展览，甲、乙、丙、丁四位同学随机分成两组乘车．

(1)、哪两位同学会被分到第一组，写出所有可能；

(2)、用列表法（或树状图法）求甲、乙分在同一组的概率．

查看试题解析
20. 如图，A、B、C为⊙O上的点，PC过O点，交⊙O于D点，PD=OD，若OB⊥AC于E点．

(1)、判断A是否是PB的中点，并说明理由；

(2)、若⊙O半径为8，试求BC的长．

查看试题解析
21.
如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，m）在边AB上，反比例函数y= $\frac{k}{x}$ （k≠0）在第一象限内的图象经过点D、E，且cos∠BOA= $\frac{4}{5}$ ．

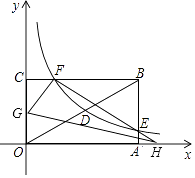(1)、求边AB的长；

(2)、求反比例函数的解析式和m的值；

(3)、若反比例函数的图象与矩形的边BC交于点F，点G、H分别是y轴、x轴上的点，当△OGH≌△FGH时，求线段OG的长．

查看试题解析
22. 某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：

①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
时间（第x天）
1
3
6
10
…
日销售量（m件）
198
194
188
180
…
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天）
1≤x＜50
50≤x≤90
销售价格（元/件）
x+60
100

(1)、求m关于x的一次函数表达式；

(2)、设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格﹣每件成本）】

(3)、在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．

查看试题解析
23. 已知△ABC中，D为AB边上任意一点，DF∥AC交BC于F，AE∥BC，∠CDE=∠ABC=∠ACB=α．

(1)、
如图1，当α=60°时，求证：△DCE是等边三角形；

(2)、
如图2，当α=45°时，求证：① $\frac{C D}{D E}$ = $\sqrt{2}$ ；②CE⊥DE．

(3)、
如图3，当α为任意锐角时，请直接写出线段CE与DE的数量关系是： $\frac{C E}{D E}$ = ．

查看试题解析

加数的个数n	S
1	2=1×2
2	2+4=6=2×3
3	2+4+6=15=3×4
4	2+4+6+8=20=4×5
5	2+4+6+8+10=30=5×6

时间（第x天）	1	3	6	10	…
日销售量（m件）	198	194	188	180	…

时间（第x天）	1≤x＜50	50≤x≤90
销售价格（元/件）	x+60	100

分数/分	7	8	9	10
频数	2	9﹣x	x+14	24